mn giải chi tiết giúp em với ạ

Có bao nhiêu giá trị $m$ để phương trình $2x+(\dfrac{\log_5x}{m+1})^2=x^2+1$ có 1 nghiệm duy nhất
ĐK: $x>0,m\ne-1$
Ta có $2x+(\dfrac{\log_5x}{m+1})^2=x^2+1$
$\Leftrightarrow (\dfrac{\log_5x}{m+1})^2=(x-1)^2$
TH1: $x=1$ thoả pt $\Rightarrow x=1$ là 1 nghiệm của pt
TH2: $x\ne1$
$\Leftrightarrow\left[\begin{matrix}
\dfrac{\log_5x}{m+1}=x-1\\
\dfrac{\log_5x}{m+1}=1-x\end{matrix}\right.
\Leftrightarrow\left[\begin{matrix}
m=\dfrac{\log_5x}{x-1}-1\\
m=-\dfrac{\log_5x}{x-1}-1\end{matrix}\right.$
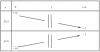
Đặt $f(x)=\dfrac{\log_5x}{x-1}-1$
$\Rightarrow f'(x)=\dfrac{-x(\ln5\log_5x)}{(x-1)^2\ln5}<0,\,\forall x>0$
Đặt $g(x)=-\dfrac{\log_5x}{x-1}-1$
$\Rightarrow g'(x)=\dfrac{x(\ln5\log_5x)}{(x-1)^2\ln5}>0,\,\forall x>0$
Bảng biến thiên bên dưới
Để phương trình đề cho có nghiệm duy nhất, thì phương trình TH2 phải vô nghiệm
Suy ra $\left[\begin{matrix}
m=\lim\limits_{x\to1}f(x)\\
m=\lim\limits_{x\to1}g(x)\end{matrix}\right.\Rightarrow
\left[\begin{matrix}
m\approx-0,3787\\
m\approx-1,6213\end{matrix}\right.$
Vậy có $2$ giá trị $m$ thoả yêu cầu đề bài, chọn câu $B$
Mình gửi bạn,có thắc mắc gì hỏi lại nha, chúc bạn học tốt
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.





