[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
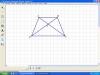
Cho hinh thang can ABCD (AB // DC)
AC cắt BD tại I
C/M: AI=IB
IC=ID
SÁNG NAY MIK ĐĂNG NHẦM ĐỀ CÁC BẠN THÔNG CẢM NHA
AC cắt BD tại I
C/M: AI=IB
IC=ID
SÁNG NAY MIK ĐĂNG NHẦM ĐỀ CÁC BẠN THÔNG CẢM NHA