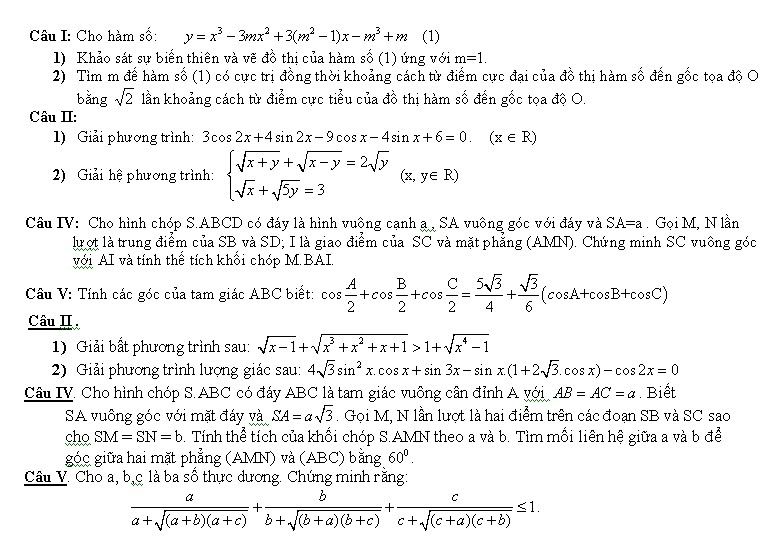Trình bày quá chi tiết, ngày xưa có thế đâu nhờ 
Câu 2:
Hình như chỗ này phải là [TEX]\sqrt{3}sin2x+cos2x=0 [/TEX]
Tính sai hay sao ý nhờ ?
Bài hình hơi vòng vo
Tính đc luôn [TEX]SH =\frac{SM.SA}{SB}[/TEX]
[TEX] ---> HP=\frac{SH.AI}{SA}[/TEX]
Còn cách nào ngắn hơn k b-(
1. a,b,c là các số thực k âm thoả mãn [TEX]a+b+c=1[/TEX]. Tìm GTLN:
[TEX]M=\frac{1+a^2}{1+b^2}+\frac{1+b^2}{1+c^2}+\frac{1+c^2}{1+a^2}[/TEX]
2. Cho 3 số dương a,b,c. CMR:
[TEX]\frac{a}{\sqrt{a^2+b^2}}+\frac{b}{\sqrt{b^2+c^2}}+\frac{c}{\sqrt{c^2+a^2}} \leq \frac{3}{\sqrt{2}}[/TEX]
Trong cả 1 thời gian ngâm cứu BDT và cực trị t thấy 2 bài này tuyệt vời nhất, cách giải đơn giản mà rất hay, mến người ra đề
3. Cho a, b,c là các số dương thoả mãn [TEX]ab+a+b=3[/TEX]. CMR
[TEX]\frac{3a}{b+1}+\frac{3b}{a+1}+\frac{a.b}{a+b} \leq a^2+b^2+\frac{3}{2}[/TEX]
Bài này hình như của trường a quyenuy , cũng hay hay 

1.
[TEX]\begin{array}{l}x = 1 + a^2 ;y = 1 + b^2 ;z = 1 + c^2 = > 3 < x + y + z \le 4;x;y;z \in \left[ {1;2} \right] \\ P = \frac{x}{y} + \frac{y}{z} + \frac{z}{x} \\ G/s:y - nam - giua - x;z \\= > \left( {\frac{x}{y} - 1} \right)\left( {\frac{y}{z} - 1} \right) \ge 0 \\\Leftrightarrow \frac{x}{y} + \frac{y}{z} \le 1 + \frac{x}{z} \\ = > P \le 1 + \frac{x}{z} + \frac{z}{x} \le \frac{7}{2} \\ = \Leftrightarrow \left( {a;b;c} \right) = \left( {0;0;1} \right);\left( {0;1;0} \right)\left( {1;0;0} \right) \\ \end{array}[/TEX]
2
[TEX]\begin{array}{l}bdt \Leftrightarrow \frac{1}{{\sqrt {1 + x} }} + \frac{1}{{\sqrt {1 + y} }} + \frac{1}{{\sqrt {1 + z} }} \le \frac{3}{{\sqrt 2 }} \\ x = \frac{{b^2 }}{{a^2 }};y = \frac{{c^2 }}{{b^2 }};z = \frac{{a^2 }}{{c^2 }} \end{array}[/TEX] với xyz=1
Ko mất tính tq giả sử z=max{x;y;z} suy ra xy<=1
Bổ đề với xy<=1 và x,y, không âm ta có
[TEX]\begin{array}{l} \frac{1}{{\sqrt {1 + x^2 } }} + \frac{1}{{\sqrt {1 + y^2 } }} \le \frac{2}{{\sqrt {1 + xy} }} \\ VT^2 \le 2\left( {\frac{1}{{1 + x^2 }} + \frac{1}{{1 + y^2 }}} \right) \le \frac{4}{{1 + xy}} \\ \end{array}[/TEX]
bđt cuối chứng minh bằng biến đổi tương đương
Do đó ta có
[TEX]\frac{1}{{\sqrt {1 + x} }} + \frac{1}{{\sqrt {1 + y} }} + \frac{1}{{\sqrt {1 + z} }} \le \frac{2}{{\sqrt {1 + \sqrt {xy} } }} + \frac{{\sqrt {xy} }}{{\sqrt {1 + xy} }} = \frac{2}{{\sqrt {1 + t} }} + \frac{t}{{\sqrt {1 + t^2 } }} = f\left( t \right),t = \sqrt {xy} \le 1[/TEX]
[TEX]f'\left( t \right) = \frac{1}{{\left( {1 + t^2 } \right)^{3/2} }} - \frac{1}{{\left( {1 + t} \right)^{3/2} }} \ge 0 = > f\left( t \right) \le f\left( 1 \right) = \frac{3}{{\sqrt 2 }}[/TEX]
Bài 3
[TEX]\begin{array}{l} gt \Leftrightarrow \left( {a + 1} \right)\left( {b + 1} \right) = 4 = > ab \le 1 \\ bdt \Leftrightarrow \frac{{3a\left( {a + 1} \right)}}{4} + \frac{{3b\left( {b + 1} \right)}}{4} + \frac{{ab}}{{a + b}} \le a^2 + b^2 + \frac{3}{2} \\VT \le \frac{3}{4}\left( {a^2 + b^2 } \right) + a + b \\ a^2 + b^2 + \frac{3}{2} -\frac{3}{4}\left( {a^2 + b^2 } \right) - a - b \ge 0 \Leftrightarrow \left( {a + b} \right)^2 - 4\left( {a + b} \right) + 4 + 2\left( {1 - ab} \right) \ge 0 \\ \end{array}[/TEX]
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.