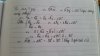[tex]\widehat{ABx'}+\widehat{BAy'}=180^{o}[/tex] (do xx' // yy' và 2 góc trong cùng phía)
[tex]\Leftrightarrow \widehat{A_{1}}+\widehat{A_{2}}+\widehat{B_{1}}+\widehat{B_{2}}=180^{o}[/tex]
[tex]\Leftrightarrow 2\widehat{A_{1}}+2\widehat{B_{1}}=180^{o}[/tex] (do [tex]\widehat{A_{1}}=\widehat{A_{2}};\widehat{B_{1}}=\widehat{B_{2}}[/tex] )
[tex]\Leftrightarrow \widehat{A_{1}}+\widehat{B_{1}}=90^{o}[/tex]
[tex]\Leftrightarrow \widehat{ACB}=180^{o}-\widehat{A_{1}}-\widehat{B_{1}}=180^{o}-90^{o}=90^{o}[/tex]
Vậy [tex]\widehat{ACB}=90^{o}[/tex]
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.