[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Hình như lời giải câu b) bài toán này, sách giáo khoa giải chưa đúng. Mong các bạn chỉ giáo giúp tôi.
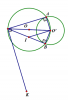
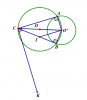
"Cho hai đường tròn (O) và (O') cắt nhau tại A và B, trong đó O' nằm trên (O). Kẻ đường kính O'OC của đường tròn (O).
a) C.minh CA, CB là các tiếp tuyến của (O').
b) Đường vuông góc với AO' tại O' cắt CB tại I. Đường vuông góc với AC tịa C cắt đường thẳng O'B ở K. Chứng minh rằng ba điểm O, I, K thẳng hàng."
Sách do NXB GDVN viết, lời giải câu b) như sau:
Theo tính chất hai tiếp tuyến cắt nhau nên: [tex]\widehat{ACO'}=\widehat{O'CB}[/tex]
Ta có CA//IO' (cùng vuông góc với AO') nên [tex]\widehat{ACO'}=\widehat{CO'I} Suy ra : \widehat{O'CI}=\widehat{CO'I}[/tex]
Do đó: tam giác ICO' cân tại I, suy ra : IC=IO' (1)
Theo tính chất hai tiếp tuyến cắt nhau nên: [tex]\widehat{AO'C}=\widehat{CO'B}[/tex].
ta có CK//AO' (do cùng vuông góc với AC) nên [tex]\widehat{AO'C}=\widehat{O'CK}[/tex]
Suy ra: [tex]\widehat{CO'B}=\widehat{O'CK}[/tex]
Do đó: KC = KO' (2)
Ta lại có: OC=OO' (3)
Từ (1), (2), và (3) suy ra 3 điểm O, I, K cùng nằm trên đường trung trực của đoạn thẳng CO', nên chúng thẳng hàng.
-----o0o------
Nhờ các bạn chú ý vùng tôi bôi đen đậm.
Nếu theo lời giải (bôi đậm) của sách bài tập này thì chẳng khác gì thừa nhận sẵn 3 điểm O', B, K thẳng hàng ngay từ đầu ?
Vì nếu ba điểm O', B, K thẳng hàng thì việc chứng minh 3 điểm O, I, K thẳng hàng trở nên quá dễ!
----
Thế nhưng đối với hình vẽ như trên nếu muốn chứng minh 3 điểm O', B, K thẳng hàng mới là điều đáng bàn, là vấn đề cần tháo gỡ; nói thẳng ra là rất khó!
Mong các bạn giúp tôi chứng minh 3 điểm O', B, K thẳng hàng. Cám ơn nhiều.
"Cho hai đường tròn (O) và (O') cắt nhau tại A và B, trong đó O' nằm trên (O). Kẻ đường kính O'OC của đường tròn (O).
a) C.minh CA, CB là các tiếp tuyến của (O').
b) Đường vuông góc với AO' tại O' cắt CB tại I. Đường vuông góc với AC tịa C cắt đường thẳng O'B ở K. Chứng minh rằng ba điểm O, I, K thẳng hàng."
Sách do NXB GDVN viết, lời giải câu b) như sau:
Theo tính chất hai tiếp tuyến cắt nhau nên: [tex]\widehat{ACO'}=\widehat{O'CB}[/tex]
Ta có CA//IO' (cùng vuông góc với AO') nên [tex]\widehat{ACO'}=\widehat{CO'I} Suy ra : \widehat{O'CI}=\widehat{CO'I}[/tex]
Do đó: tam giác ICO' cân tại I, suy ra : IC=IO' (1)
Theo tính chất hai tiếp tuyến cắt nhau nên: [tex]\widehat{AO'C}=\widehat{CO'B}[/tex].
ta có CK//AO' (do cùng vuông góc với AC) nên [tex]\widehat{AO'C}=\widehat{O'CK}[/tex]
Suy ra: [tex]\widehat{CO'B}=\widehat{O'CK}[/tex]
Do đó: KC = KO' (2)
Ta lại có: OC=OO' (3)
Từ (1), (2), và (3) suy ra 3 điểm O, I, K cùng nằm trên đường trung trực của đoạn thẳng CO', nên chúng thẳng hàng.
-----o0o------
Nhờ các bạn chú ý vùng tôi bôi đen đậm.
Nếu theo lời giải (bôi đậm) của sách bài tập này thì chẳng khác gì thừa nhận sẵn 3 điểm O', B, K thẳng hàng ngay từ đầu ?
Vì nếu ba điểm O', B, K thẳng hàng thì việc chứng minh 3 điểm O, I, K thẳng hàng trở nên quá dễ!
----
Thế nhưng đối với hình vẽ như trên nếu muốn chứng minh 3 điểm O', B, K thẳng hàng mới là điều đáng bàn, là vấn đề cần tháo gỡ; nói thẳng ra là rất khó!
Mong các bạn giúp tôi chứng minh 3 điểm O', B, K thẳng hàng. Cám ơn nhiều.
