Toán 12 Xét tính đơn điệu

[tranngocbaonguyen111@gmail.com]

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

anh chị hướng dẫn em làm bài này với ạ...

 

[matheverytime]

[tex]g'(x)=f(x)+xf'(x)[/tex]
để hàm số [TEX]g'(x)[/TEX] đồng biến thì [TEX] f(x)>0[/TEX] và [TEX]xf'(x)>0[/TEX]
ta có bảng biến thiên

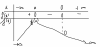
[TEX]a[/TEX] trong đồ thị thảo [TEX]a<-3[/TEX] ( [TEX]a[/TEX] là điểm [TEX]f'(x) =0[/TEX] em nhìn đồ thị giả sử nhé )
để [TEX]f(x) >0[/TEX] thì [TEX]x[/TEX] chắc chăn thuộc khoảng [TEX](a;0)[/TEX]
để [TEX]xf'(x)>0[/TEX] TH1: [TEX]x>0[/TEX] và [TEX]f'(x)>0 => x<a[/TEX] => ( vô lý )
TH2: [TEX]x<0[/TEX] và [TEX]f'(x)<0[/TEX] => [TEX]x>a => x[/TEX] thuộc [TEX](a;0)[/TEX]
=> để [TEX]g'(x) >0[/TEX] thì [TEX]x[/TEX] thuộc [TEX] (a;0)[/TEX] mà [TEX]a<-3[/TEX] => B đúng nhất