Toán 10 Xác định vị trí của điểm M trên cung lớn CD để khoảng cách từ D đến tâm O' nhỏ nhất

[Lê Linh 1310]

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

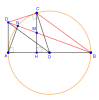
1. Cho đường tròn tâm O đường kính AB. Điểm C thay đổi trên đường tròn O không trùng với A,B. Kẻ CH vuông góc với AB tại H. Các tiếp tuyến với đường tròn O tại A và C cắt nhau tại D. Đường thẳng DB cắt CH tại M và cắt đường tròn O tại điểm thứ hai là N.
a) cm : tg AHMN là tgnt
b) CM : BC // OD
c) cm : M là trung điểm của HC
d) Xác định vị trí của C trên đường tròn O để diện tích tam giác BCD lớn nhất
các bạn giúp mình câu d nha, mấy câu kia mình làm đc rồi !!!!
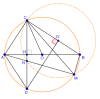
2. Cho đường tròn O đường kính AB cố định, Điểm H cố định thuộc đoạn thẳng AO ( H khác A và B ). Dây cung CD cuông góc với AB tại H. Điểm M thay đổi trên cung lớn CD. Đường thẳng AM cắt CD tại N
a) tg HBMN là tgnt
b) MA là tia pg góc CMD
c) Gọi O' là tâm của đường tròn ngoại tiếp tam giác CMN. cm : CA là tiếp tuyến của đường tròn O'. Xác định vị trí của điểm M trên cung lớn CD để khoảng cách từ D đến tâm O' nhỏ nhất
mình còn câu c chưa giải đc, các bạn giúp mình nhé

 

[iceghost]

1d) Có $S_{BCD} = S_{BCO}$ (do $DO \parallel CB$)
Mà $S_{BCO} = \dfrac12 OC \cdot OB \cdot \sin \widehat{BOC} \leqslant \dfrac12 R^2 \cdot 1 = \dfrac12 R^2$
Dấu '=' xảy ra khi $\widehat{BOC} = 90^\circ$...

 

[iceghost]

2c) Do $\widehat{ACN} = \widehat{AMD} = \widehat{AMC}$ nên $AC$ là tiếp tuyến của $(O')$ ngoại tiếp tam giác $CMN$
$\implies O'C \perp CA$, mà $BC \perp CA$ nên $O'$ nằm trên $CB$
Để $DO'$ ngắn nhất thì $DO' \perp BC$. Do đó kẻ $DO_1 \perp BC$, khi đó khi $M$ là giao điểm thứ hai của $(O_1,O_1C)$ và $(O)$ thì $DO'$ sẽ ngắn nhất...