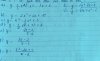g) TXD: $D = \mathbb{R} \setminus 2$
$y = \dfrac{x^2 - 2x + 1}{x - 2}$
$y' = \dfrac{x^2 - 4x + 3}{(x - 2)^2}$
$
\begin{array}{c|ccccccccccc}
x & -\infty & & 1 & & & 2 & & & 3 & & +\infty \\
\hline
y' & & + & 0 & - & & || & & - & 0 & + \\
\hline
& & & 0 & & & || & +\infty & & & & +\infty \\
& & \nearrow & & \searrow & & || & & \searrow & & \nearrow & \\
y & -\infty & & & & -\infty & || & & & 4 & &
\end{array}
$
h) TXD: $D= (-\infty , 1] \cup [7, +\infty)$
$y = \sqrt{x^2 - 8x + 7}$
$y' = \dfrac{2x - 8}{2\sqrt{x^2 - 8x + 7}}$
$
\begin{array}{c|ccccccc}
x & -\infty & & 1 & |/////| & 7 & & +\infty \\
\hline
y' & & - & & |/////| & & + \\
\hline
y & +\infty & & & |/////| & & & +\infty \\
& & \searrow & & |/////| & & \nearrow & \\
& & & 0 & |/////| & 0 & &
\end{array}
$
(Phần giữa gạch sọc)
i) Tương tự $h$
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
