leduymanh2005
Tần số góc của con lắc lò xo: [imath]\omega = \sqrt{\dfrac{k}{m}}=10\pi \ rad/s[/imath]
[imath]v_{max}=\omega A \Rightarrow A=5cm[/imath]
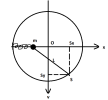
Chọn gốc [imath]O[/imath] như hình vẽ, trục [imath]Ox[/imath] nằm ngang sang phải. [imath]t=0[/imath] là lúc trạng thái con lắc lò xo và điểm [imath]S[/imath] như đề ra.
Phương trình dao động của lò xo: [imath]x=5\cos(10\pi t \pm \dfrac{\pi}{2})[/imath]
giả sử qua vị trí cân bằng theo chiều dương thì [imath]x=5\cos(10\pi t - \dfrac{\pi}{2})[/imath]
[imath]S_x = 5\cos 10\pi t[/imath]
[imath]S_y = 5\sin 10\pi t[/imath]
Khoảng cách giữa [imath]m[/imath] và [imath]S[/imath]:
[imath]L^2 = S_y^2 + (S_x -x)^2 = 25 \sin ^2 10\pi t +50\cos ^2 (10\pi t -\dfrac{\pi}{4})[/imath]
[imath]=25.(\dfrac{1-\cos 20\pi t}{2})+50.(\dfrac{1+\cos(20\pi t -\dfrac{\pi}{2})}{2})[/imath]
[imath]=37,5 -\dfrac{25}{2}\cos 20\pi t +25\sin 20\pi t[/imath]
[imath]=37,5 + \dfrac{25\sqrt{5}}{2}[\dfrac{2\sqrt{5}}{5}\sin 20\pi t -\dfrac{\sqrt{5}}{5}\cos 20\pi t][/imath]
[imath]=37,5 +\dfrac{25\sqrt{5}}{2}\sin (20\pi t +\alpha)[/imath]
Với [imath]\sin \alpha = \dfrac{-\sqrt{5}}{5}[/imath] và [imath]\cos \alpha = \dfrac{2\sqrt{5}}{5}[/imath]
[imath]\le 37,5 + \dfrac{25\sqrt{5}}{2}.1 =\dfrac{75+25\sqrt{5}}{2}[/imath]
[imath]\Rightarrow L_{max} \approx 8,09 cm[/imath] |
 |
Chúc bạn học tốt!
-----
Xem thêm:
Tổng hợp những điều quan trọng trong chương Dao động cơ
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.