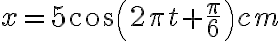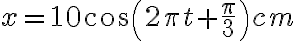H
hocmai.vatli
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
1. Định nghĩa và phương trình dao động điều hòa:
Dao động mà phương tình có dạng x = Acos(ωt + φ) hoặc x = Asin(ωt + φ) gọi là dao động điều hòa.
Pt dao động điều hòa là: x = Acos(ωt + φ) hoặc x = Asin(ωt + φ).
2. Các đại lượng đặc trưng của dao động điều hòa:
- Li độ x là khoảng lệch của vật khỏi vị trí cân bằng.
- Biên độ A là giá trị cực đại của li độ x. Hoặc là độ lệch cực đại của vật khỏi vị trí cân bằng. Biên độ A luôn có giá trị dương.
- Pha dao động là: ωt + φ, và pha ban đầu là: φ. Với một biên độ đã cho thì pha xác định li độ x của dao động.
- Tần số góc ω của dao động. Hay là tốc độ biến đổi của góc pha. Đơn vị là rad/s. Với một con lắc lò xo đã cho thì tần số góc chỉ có giá trị xác định bởi công thức: [TEX]\omega^2 = \frac{k}{m}[/TEX].
3. Chu kì và tần số
+ ĐN:
Chu kì là khoảng thời gian ngắn nhất sau đó trạng thái dao động lặp lại như cũ, hay khoảng thời để vật thực hiện được một dao động toàn phần.
Tần số là số dao động toàn phần mà vật thực hiện được trong 1 đơn vị thời gian (Hz).
+ Công thức: T = 1/N = 2π/ω; f = 1/T = ω/2π; ω = 2πf;
4. Vận tốc: v = x' = -ωA = -ωAsin(ωt + φ).
Vận tốc đạt giá trị cực đại là: vmax = ωA khi vật ở vị trí cân bằng.
5. Gia tốc: [TEX]a = - \omega ^2 x = - \omega ^2 A\cos \left( {\omega t + \varphi } \right)\left( {m/s^2 } \right)[/TEX]
Gia tốc luôn hướng về vị trí cân bằng. Gia tốc đạt cực đại khi vật ở vị trí biên.
6. Công thức độc lập: [TEX]A^2 = x^2+ \frac{{\upsilon ^2 }}{{\omega ^2 }}[/TEX]
7. Định luật bảo toàn cơ năng: Trong quá trình doa động điều hòa luôn có sự biến đổi qua lại giữa động năng và thế năng, nếu động năng tăng thì thế năng giảm và ngược lại, nhưng cơ năng luôn được bảo toàn va tỉ lệ với bình phương biên độ dao động.
8. Lực tác dụng: Luôn hướng về vị trí cân bằng. F = k(Δl + x)
Fmin = k|Δl - A|. Nếu Δl > A thì Fmin = k(Δl -A)
Nếu Δl < A thì Fmin = 0
Fmax = k(Δl + A)
Dao động mà phương tình có dạng x = Acos(ωt + φ) hoặc x = Asin(ωt + φ) gọi là dao động điều hòa.
Pt dao động điều hòa là: x = Acos(ωt + φ) hoặc x = Asin(ωt + φ).
2. Các đại lượng đặc trưng của dao động điều hòa:
- Li độ x là khoảng lệch của vật khỏi vị trí cân bằng.
- Biên độ A là giá trị cực đại của li độ x. Hoặc là độ lệch cực đại của vật khỏi vị trí cân bằng. Biên độ A luôn có giá trị dương.
- Pha dao động là: ωt + φ, và pha ban đầu là: φ. Với một biên độ đã cho thì pha xác định li độ x của dao động.
- Tần số góc ω của dao động. Hay là tốc độ biến đổi của góc pha. Đơn vị là rad/s. Với một con lắc lò xo đã cho thì tần số góc chỉ có giá trị xác định bởi công thức: [TEX]\omega^2 = \frac{k}{m}[/TEX].
3. Chu kì và tần số
+ ĐN:
Chu kì là khoảng thời gian ngắn nhất sau đó trạng thái dao động lặp lại như cũ, hay khoảng thời để vật thực hiện được một dao động toàn phần.
Tần số là số dao động toàn phần mà vật thực hiện được trong 1 đơn vị thời gian (Hz).
+ Công thức: T = 1/N = 2π/ω; f = 1/T = ω/2π; ω = 2πf;
4. Vận tốc: v = x' = -ωA = -ωAsin(ωt + φ).
Vận tốc đạt giá trị cực đại là: vmax = ωA khi vật ở vị trí cân bằng.
5. Gia tốc: [TEX]a = - \omega ^2 x = - \omega ^2 A\cos \left( {\omega t + \varphi } \right)\left( {m/s^2 } \right)[/TEX]
Gia tốc luôn hướng về vị trí cân bằng. Gia tốc đạt cực đại khi vật ở vị trí biên.
6. Công thức độc lập: [TEX]A^2 = x^2+ \frac{{\upsilon ^2 }}{{\omega ^2 }}[/TEX]
7. Định luật bảo toàn cơ năng: Trong quá trình doa động điều hòa luôn có sự biến đổi qua lại giữa động năng và thế năng, nếu động năng tăng thì thế năng giảm và ngược lại, nhưng cơ năng luôn được bảo toàn va tỉ lệ với bình phương biên độ dao động.
8. Lực tác dụng: Luôn hướng về vị trí cân bằng. F = k(Δl + x)
Fmin = k|Δl - A|. Nếu Δl > A thì Fmin = k(Δl -A)
Nếu Δl < A thì Fmin = 0
Fmax = k(Δl + A)
Last edited by a moderator: