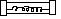Cho 2 vật như hình vẽ, lò xo độ cứng k, bỏ qua khối lượng, lò xo bị nén bởi 2 dây, 2 vật nặng khối lượng là m1, m2. Đốt 2 dây nối, chứng minh dao động điều hòa và tính chu kì trong 3 trường hợp
a) ban đầu 2 vật được thả tự do
b) ban đầu 1 vật được giữ cố định
c) ban đầu 1 vật tì vào tường
Ban đầu hai vật được thả tự do.
Gọi L là chiều dài lò xo.
Chọn hệ quy chiếu gắn với khối tâm G (khối tâm không đổi).
Lúc này xem hệ như hai con lắc với hai lò xo độc lập giá là G.
Khối tâm G cách con lắc 1 một đoạn [TEX]L_1 = \frac{m_2L}{m_1+m_2}[/TEX]
cách con lắc 2 một đoạn [TEX]L_2 = \frac{m_1L}{m_1+m_2}[/TEX]
Độ cứng của lò xo1: [TEX]K_1 = \frac{Lk}{L_1} = \frac{k(m_1+m_2)}{m_2}[/TEX]
Độ cứng của lò xo2: [TEX]K_2 = \frac{Lk}{L_2} = \frac{k(m_1+m_2)}{m_1}[/TEX]
Chứng minh con lắc dao động điều hoà.
Với con lắc 1.
Giả sử ban đầu [TEX]m_1[/TEX] Xét tại vị trí cách vị trí cân bằng một đoạn x.
Năng lượng bảo toàn.
[TEX]\frac{K_1x^2}{2} + \frac{m_1V^2}{2} = const[/TEX]
Lấy đạo hàm hai vế.
[TEX]\frac{K_1x*x'}{2} + \frac{m_1v*v'}{2} = 0[/TEX]
Vì [TEX]x' = v[/TEX], [TEX]v' = x^{''}[/TEX] ta được:
[TEX]K_1x + m_1x^{''} = 0[/TEX]
Hay [TEX]\frac{xK_1}{m_1} + x^{''} = 0 \Leftrightarrow x\frac{k(m_1+m_2)}{m_1m_2}+x^{''} = 0[/TEX]
Con lắc 2 tương tự. Ta tìm được chu kì [TEX]T = 2\pi\sqrt[]{\frac{m_1m_2}{K(m_1+m_2)}}[/TEX].
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.