S
sakuramine
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
có 2 bài này em thấy khó wa' nhờ mọi người giải giúp:
1/
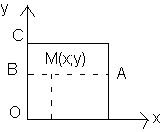
một cái bàn vuông nhẹ có bốn chân giống nhau. Nếu đặt vật có trọng lượng wa' 2P đúng giữa bàn thì chân bàn gãy. Tìm các điểm có thể đặt vật trọng lượng P mà chân bàn không gãy.
2/
trong chiếc mô tô bay, một người đi mô tô trên thành hình trụ thẳng đứng bán kính r=9m. Khối tâm người và xe cách thành trụ h=1m và vạch một đường tròn nằm ngang, cận tốc 20m/s. Tìm góc ngiêng alpha của xe với phươn ngang. (đs bài này là: 11 độ)
1/
một cái bàn vuông nhẹ có bốn chân giống nhau. Nếu đặt vật có trọng lượng wa' 2P đúng giữa bàn thì chân bàn gãy. Tìm các điểm có thể đặt vật trọng lượng P mà chân bàn không gãy.
2/
trong chiếc mô tô bay, một người đi mô tô trên thành hình trụ thẳng đứng bán kính r=9m. Khối tâm người và xe cách thành trụ h=1m và vạch một đường tròn nằm ngang, cận tốc 20m/s. Tìm góc ngiêng alpha của xe với phươn ngang. (đs bài này là: 11 độ)