[Vật lí 10] - Bài tập cđ thẳng đều

[heroineladung]

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

Bài tập:

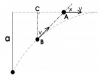
Hai tàu A và B cách nhau một khoảng cách a đồng thời chuyển động thẳng đều với vận tốc lớn v của vận tốc từ hai nơi trên một bờ hồ thẳng.
Tàu A chuyển động theo hướng vuông góc với bờ trong khi tàu B luôn luôn hướng về tàu A. Sau một thời gian đủ lâu, tàu B và tàu A chuyển động trên cùng một đường thẳng nhưng cách nhau một khoảng không đổi.
Tính khoảng cách này.

ĐS: [TEX]d = \frac{a}{2}[/TEX]

Mọi người ơi, giúp mình (em) bài này với, bài này chỉ có đáp số không có bài giải nên mình không hiểu gì hết. Ai làm được bài này thì giải chi tiết ra dùm mình (em) với nhé! Cám ơn mọi người rất nhiều! :x

 

[hunter3d10]

Tại một thời điểm nào đó thì vị trí các tàu như thế này

Gọi x là góc hợp giữa đường nối 2 thuyền và vecto vận tốc thuyền A
*************
Khi ấy
Thứ nhất: Chiếu các vecto vận tốc theo phương nối 2 tàu (phương AB) thì
Tàu B tiến lại gần tàu A với tốc độ v(1-cosx)
Thứ hai : Chiếu các vecto vận tốc theo phương ngang (phương AC) thì
Tàu A đi xa tàu B theo phương ngang với tốc độ v(1-cosx)
**************
Như vậy, trong cùng 1 khoảng thời gian rất nhỏ. Tàu B tiến lại gần A theo phương AB 1 đoạn bao nhiêu thì tàu A lại rời xa tàu B theo phương ngang 1 đoạn bấy nhiêu===> tức là tổng khoảng cách AB+AC là không đổi
**************
Sau 1 thời gian đủ lâu thì 2 tàu sẽ cùng nằm trên đường AC. Mawcj dù điều này nói chính xác là sai vì theo cách đi như vậy tàu B chỉ dần dần tiếp tuyến với AC chứ không bao giờ nằm trên AC được. Nhưng nếu xét theo thực tế thì khi khoảng cách BC chỉ còn vài mm thì ta có thể coi như nó đã năm trên AC.
**********************
Khi ấy AC=AB. Mà lúc đầu AC+AB=a==> sau 1 thời gian đủ lâu khoảng cách giữa 2 tàu là a\2

 

[anime1234567]

@baogiang0304 ,@tieutukeke,@Trai Họ Nguyễn,@Monkey.D.Yato/.....làm ơn gải thik giùm e vs ...soa mk anh kia lmf ra v nhân vs 1-cosx vậy ạ

 

[Dinhnhat1432003]

Em cũng ko hiểu đc ạ ? Mong mọi ng giải thik hộ e vs

 

[anime1234567]

Em cũng ko hiểu đc ạ ? Mong mọi ng giải thik hộ e vs

bạn chưa hiểu chỗ nào z ak

 

[vanhoangk27]

khó hiểu ...................

 

[Linh Huyền]

Tại một thời điểm nào đó thì vị trí các tàu như thế này

Gọi x là góc hợp giữa đường nối 2 thuyền và vecto vận tốc thuyền A
*************
Khi ấy
Thứ nhất: Chiếu các vecto vận tốc theo phương nối 2 tàu (phương AB) thì
Tàu B tiến lại gần tàu A với tốc độ v(1-cosx)
Thứ hai : Chiếu các vecto vận tốc theo phương ngang (phương AC) thì
Tàu A đi xa tàu B theo phương ngang với tốc độ v(1-cosx)
**************
Như vậy, trong cùng 1 khoảng thời gian rất nhỏ. Tàu B tiến lại gần A theo phương AB 1 đoạn bao nhiêu thì tàu A lại rời xa tàu B theo phương ngang 1 đoạn bấy nhiêu===> tức là tổng khoảng cách AB+AC là không đổi
**************
Sau 1 thời gian đủ lâu thì 2 tàu sẽ cùng nằm trên đường AC. Mawcj dù điều này nói chính xác là sai vì theo cách đi như vậy tàu B chỉ dần dần tiếp tuyến với AC chứ không bao giờ nằm trên AC được. Nhưng nếu xét theo thực tế thì khi khoảng cách BC chỉ còn vài mm thì ta có thể coi như nó đã năm trên AC.
**********************
Khi ấy AC=AB. Mà lúc đầu AC+AB=a==> sau 1 thời gian đủ lâu khoảng cách giữa 2 tàu là a\2

hình như phải là căn của 2 x (1-cosx) chứ

 

[Linh Huyền]

mà chuyển động thẳng đều mà

 

[Thu trang _2216]

giả sử tại 1 thời điểm, tàu A và B có vị trí như hình vẽ [tex]\underset{AB}{\rightarrow}[/tex] hộ với Ox 1 góc [tex]\alpha[/tex]
C là hình chiếu của B trên phương Ox
Xét phương Ox:
Vận tốc của C :[tex]v_{C}=v.cos\alpha[/tex]
Khoảng cách AC theo thời gian sẽ tăng 1 lượng :[tex]v-v.cos\alpha[/tex]
Xét phương AB:
Vận tốc của điểm A trên phương AB:[tex]v_{A}=v.cos\alpha[/tex]
Khoảng cách AB theo thời gian sẽ giảm 1 lượng :[tex]v-v.cos\alpha[/tex]
Hay suy ra AB+AC không đổi
Tại thời điểm ban đầu AB=a, AC=0 , AB+AC=a
Tại thời điểm 2 tàu thẳng hàng B trùng C nên AC=AB [tex]\Rightarrow AB=\frac{a}{2}[/tex]

 

[Lê Hùng 2003]

View attachment 77511
giả sử tại 1 thời điểm, tàu A và B có vị trí như hình vẽ [tex]\underset{AB}{\rightarrow}[/tex] hộ với Ox 1 góc [tex]\alpha[/tex]
C là hình chiếu của B trên phương Ox
Xét phương Ox:
Vận tốc của C :[tex]v_{C}=v.cos\alpha[/tex]
Khoảng cách AC theo thời gian sẽ tăng 1 lượng :[tex]v-v.cos\alpha[/tex]
Xét phương AB:
Vận tốc của điểm A trên phương AB:[tex]v_{A}=v.cos\alpha[/tex]
Khoảng cách AB theo thời gian sẽ giảm 1 lượng :[tex]v-v.cos\alpha[/tex]
Hay suy ra AB+AC không đổi
Tại thời điểm ban đầu AB=a, AC=0 , AB+AC=a
Tại thời điểm 2 tàu thẳng hàng B trùng C nên AC=AB [tex]\Rightarrow AB=\frac{a}{2}[/tex][/QUO

Cho mình hỏi là [tex]Vc = V.\cos \alpha[/tex] là gì vậy

 

[tranhuyhoangvipvd5]

bài này sử dụng đạo ham ez

 

[Vie Hoàng]

Hình như góc [tex]\alpha[/tex] nó thay đổi liên tục mà