$DK:x>0$
BPT tương đương [tex](y-x)(log_2x+x-3)>0[/tex]
Xét hàm [tex]f(x)=log_2x+x-3\\f'(x)=\frac{1}{x.ln2}+1>0 \forall x>0[/tex]
Vậy hàm đồng biến trên $(0;+\infty)$ , nhận thấy $x=2$ là nghiệm của PT $f(x)=0$, do hàm đồng biến trên $(0;+\infty)$ nên $x=2$ là nghiệm duy nhất, ta có BBT:
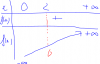
Vậy từ BPT suy được 2 TH:
TH1: $
\left\{\begin{matrix}
& y>x & \\
& x>2 &
\end{matrix}\right.\Leftrightarrow 2<x<y
$
Do y nguyên dương , để không quá 2019 giá trị nguyên của x thì ta có: [tex]y=\begin{Bmatrix} 3,4,...,2022 \end{Bmatrix}[/tex]
TH2:
$
\left\{\begin{matrix}
& y<x & \\
& x<2 &
\end{matrix}\right.\Leftrightarrow y<x<2
$
TH này chỉ có duy nhất $y=1$ thoả đề
Vậy có 2021 giá trị y thoả đề
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
