$g'(x)=2f'(x)+2x$
Kẻ đường thẳng $y=-x$ vào trong hình:
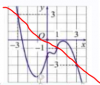
KS hàm $g(x)$:
$
\begin{array}{c|ccccccccc}
x & -\infty & & -3 & & 1 & & 3 & & +\infty \\
\hline
y' & & + & 0 & - & 0 & + & 0 & - \\
\hline
& & & g(-3) & & & & g(3) & & \\
& & \nearrow & & \searrow & & \nearrow & & \searrow & \\
y & -\infty & & & & -43 & & & & -\infty
\end{array}
$
Diện tích hình phẳng giới hạn bởi $y=f'(x); y=-x; x=-3 ; x=1$ lớn hơn diện tích hình phẳng giới hạn bởi $y=f'(x); y=-x ; x=1; x=3$
Do đó [tex]\int ^1_{-3}(-f'(x)-x )dx>\int ^3_1( f'(x) + x) dx\\\Leftrightarrow g(-3)-g(1)>g(3)-g(1)\\\Leftrightarrow g(-3)>g(3)[/tex]
Dễ thấy diện tích hình phẳng giới hạn bởi $y=f'(x); y=-x; x=-3 ; x=1$ nhỏ hơn diện tích tam giác và hình vuông như hình
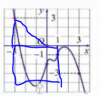
Mỗi ô vuông ứng với 1 đơn vị nên có $S=1$ Do đó:
[tex]\int ^1_{-3}(-f'(x)-x )dx< 16+4,5\\\Leftrightarrow \frac{1}{2}(g(-3)-g(1))<20,5\\\Leftrightarrow \frac{1}{2}g(-3)+\frac{43}{2}<20,5\\\Leftrightarrow g(-3)<-2[/tex]
Như vậy $g(-3)<0$
PT vô nghiệm, chọn D
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
