- 9 Tháng tư 2020
- 1,049
- 1,064
- 181
- 19
- Hải Dương
- THPT Chuyên Nguyễn Trãi
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Hello mọi người ^^
Ai đã trải qua giai đoạn thi vào lớp 10 chắc hẳn đều biết nó khó như nào phải không?
Là một trong những môn học quan trọng, đề thi toán thường có những ý được đánh giá là để khó lấy điểm 9,10. Trong đó có một ý thuộc phần hình học: Đường tròn.
Cùng mình phân tích một số thế hình thường xuất hiện trong các đề thi vào 10 nhé! :3
Thế hình 1: Tam giác nội tiếp đường tròn có 3 đường cao.
Xét tam giác ABC nội tiếp (O;R). AD,BE,CF là ba đường cao. H là trực tâm.
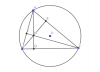
- Từ thế hình này, ta trực tiếp suy ra [tex]AD\perp BC;BE\perp AC;CF\perp AB[/tex]
[tex]\Rightarrow[/tex] Các tứ giác nội tiếp BCEF;ABDE;ACDF ( có 2 đỉnh cùng kề một cạnh, cùng nhìn 1 cạnh với góc bằng 90 độ)
Các tứ giác nội tiếp BDHF;AEHF;CEHD (có 2 góc đối nhau bằng 90 độ)
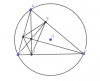
- Xét các cặp góc bằng nhau (dựa vào các tứ giác nội tiếp) , ta suy ra được:
DH là phân giác của [tex]\widehat{EDF}[/tex]
EH là phân giác của [tex]\widehat{FED}[/tex]
FH là phân giác của [tex]\widehat{EFD}[/tex]
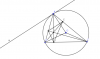
- Dễ dàng nhận thấy [tex]OA\perp EF;OB\perp DF;OC\perp ED[/tex]
Để chứng minh [TEX]OA\perp EF[/TEX] ta có thể dựa vào việc chứng minh EF song song tiếp tuyến của (O;R) tại A là Aa vì [TEX]Aa\perp OA[/TEX].
Có [tex]\bigtriangleup ABE\sim \bigtriangleup ACF(g.g)[/tex]
[tex]\Leftrightarrow \frac{AB}{AC}=\frac{AE}{AF}[/tex]
[tex]\Rightarrow \bigtriangleup ABC\sim \bigtriangleup AEF(c.g.c)[/tex]
[tex]\Leftrightarrow \widehat{AFE}=\widehat{ACB}[/tex]
Lại có [tex]\widehat{ACB}=\widehat{BAa}[/tex] (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung chắn cung AB)
Suy ra [tex]\widehat{AFE}=\widehat{BAa}\Rightarrow EF//Aa[/tex] (2 góc so le trong)
-Từ đó ta dễ dàng đưa ra đẳng thức [tex]S_{ABC}=S_{AEOF}+S_{BDOF}+S_{CDOE}=\frac{R}{2}(EF+DE+DF)[/tex]
Đây mới chỉ là những điều được suy ra và chứng minh từ thế hình cơ bản. Nếu thêm một số điều kiện khác thì sẽ ra sao nhỉ? Hẹn các bạn 3 ngày sau nhé!^^
Chúc các bạn một buổi tối vui vẻ nha!
Ai đã trải qua giai đoạn thi vào lớp 10 chắc hẳn đều biết nó khó như nào phải không?
Là một trong những môn học quan trọng, đề thi toán thường có những ý được đánh giá là để khó lấy điểm 9,10. Trong đó có một ý thuộc phần hình học: Đường tròn.
Cùng mình phân tích một số thế hình thường xuất hiện trong các đề thi vào 10 nhé! :3
Thế hình 1: Tam giác nội tiếp đường tròn có 3 đường cao.
Xét tam giác ABC nội tiếp (O;R). AD,BE,CF là ba đường cao. H là trực tâm.
- Từ thế hình này, ta trực tiếp suy ra [tex]AD\perp BC;BE\perp AC;CF\perp AB[/tex]
[tex]\Rightarrow[/tex] Các tứ giác nội tiếp BCEF;ABDE;ACDF ( có 2 đỉnh cùng kề một cạnh, cùng nhìn 1 cạnh với góc bằng 90 độ)
Các tứ giác nội tiếp BDHF;AEHF;CEHD (có 2 góc đối nhau bằng 90 độ)
- Xét các cặp góc bằng nhau (dựa vào các tứ giác nội tiếp) , ta suy ra được:
DH là phân giác của [tex]\widehat{EDF}[/tex]
EH là phân giác của [tex]\widehat{FED}[/tex]
FH là phân giác của [tex]\widehat{EFD}[/tex]
- Dễ dàng nhận thấy [tex]OA\perp EF;OB\perp DF;OC\perp ED[/tex]
Để chứng minh [TEX]OA\perp EF[/TEX] ta có thể dựa vào việc chứng minh EF song song tiếp tuyến của (O;R) tại A là Aa vì [TEX]Aa\perp OA[/TEX].
Có [tex]\bigtriangleup ABE\sim \bigtriangleup ACF(g.g)[/tex]
[tex]\Leftrightarrow \frac{AB}{AC}=\frac{AE}{AF}[/tex]
[tex]\Rightarrow \bigtriangleup ABC\sim \bigtriangleup AEF(c.g.c)[/tex]
[tex]\Leftrightarrow \widehat{AFE}=\widehat{ACB}[/tex]
Lại có [tex]\widehat{ACB}=\widehat{BAa}[/tex] (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung chắn cung AB)
Suy ra [tex]\widehat{AFE}=\widehat{BAa}\Rightarrow EF//Aa[/tex] (2 góc so le trong)
-Từ đó ta dễ dàng đưa ra đẳng thức [tex]S_{ABC}=S_{AEOF}+S_{BDOF}+S_{CDOE}=\frac{R}{2}(EF+DE+DF)[/tex]
Đây mới chỉ là những điều được suy ra và chứng minh từ thế hình cơ bản. Nếu thêm một số điều kiện khác thì sẽ ra sao nhỉ? Hẹn các bạn 3 ngày sau nhé!^^
Chúc các bạn một buổi tối vui vẻ nha!
Last edited:
