Xin chào mọi người!
Em là thành viên mới ,mong mọi người giúp đỡ
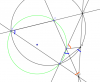
Em có 1 bài khó mà nghĩ mãi không ra, cả nhà giúp em với ạ : cho tứ giác ABCD nội tiếp đường tròn , AD giao BC tại E , AB giao CD ở F. Mà là giáo điểm của EF với đường tròn ngoại tiếp tam giác ABE. Chứng minh AE.ED=EF.EM
Bạn tự vẽ hình cho bài toán. Hoặc xem hình ở file dưới.
Rõ ràng là cần phải c/m 2 tam giác EMD và EAF đồng dạng đúng ko.
Bài này chủ yếu cho các giao điểm của các đường thẳng, đường tròn, nên ta nghĩ đến cách dùng các góc để chỉ ra bằng nhau.
2 tam giác trên đồng dạng nghĩa là các góc cũng = nhau, nghĩa là ta cũng có góc EDM = góc EFA
mà góc EDM + góc MDA = 180 độ do E, D, A thẳng hàng. có nghĩa là góc MDA + góc MFA cũng phải = 180 độ, hay tứ giác MDAF nội tiếp đúng ko.
Để c/m tứ giác này nội tiếp, ta nghĩ đến việc c/m 2 góc cùng nhìn 1 cạnh bằng nhau.
ta thử xét 2 góc ADF và AMF xem sao? liệu chúng có cùng = 1 góc thứ 3 nào đó hay ko? Có, đó chính là góc B của tứ giác ABCD. Bạn dễ nhìn thấy điều này đúng ko do bởi ABCD và ABEM là các tứ giác nội tiếp.
Trong hình học phẳng, có các khái niệm sau, bạn hãy thử suy nghĩ kĩ xem chúng có các mối quan hệ ntn?
- Mặt phẳng (tất nhiên rồi, mọi đối tượng hình học đều nằm trên mặt phẳng)
- Điểm
- Đường thẳng
- Tia
- Đoạn thẳng
- Góc (nhọn, vuông, tù, bẹt)
- Các hình: tam giác, tứ giác (các hình đặc biệt như thang, bình hành, thoi, chữ nhật, vuông, ..), đa giác, đường tròn, đường elip, đường cong khác (parabol, hypebol, đường cong phức tạp, ...)
- Các quan hệ: Cùng phía khác phía, thuộc, song song, vuông góc, thẳng hàng, đồng quy, ...
- Các tính chất khác: Các định lý, tính chất liên quan đến các đối tượng trên.
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
