Toán 10 Tứ giác điều hoà

[Windeee]

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

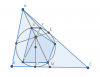
Cho tam giác ABC trung tuyến AM cắt đường tròn nội tiếp (I) tại X,Y. Các điểm Z,T thuộc (I) sao cho XZ//YT//BC. Đường thẳng AZ giao với (I) tại điểm thứ hai là J. Chứng minh rằng tứ giác JYTX là tứ giác điều hoà.
Sử dụng bổ đề: Các tiếp điểm với BC,CA,AB lần lượt là D,E,F, DI cắt EF tại N. Khi đó, AN đi qua trung điểm BC.

 

[7 1 2 5]

Chứng minh bổ đề: (cách lớp 9)
Vẽ đường thẳng qua N song song với BC cắt AB, AC tại P, Q; vẽ IH vuông góc với EF tại H.
Ta chứng minh được [TEX]\Delta IHF \sim \Delta INP, \Delta IHE \sim \Delta INQ \Rightarrow \frac{HF}{NP}=\frac{IH}{IN}=\frac{HE}{NQ}[/TEX]
Mà [TEX]HE=HF \Rightarrow NP=NQ[/TEX] nên theo định lí Thales ta có N thuộc AM.

Quay lại bài toán:
Nhận thấy [TEX]XZYT[/TEX] là hình thang cân nội tiếp [TEX](I)[/TEX], giả sử XY cắt ZT tại N' thì N' thuộc trung trực của 2 đáy.
Mà [TEX]ID \perp YT, IT=IY[/TEX] nên ID là trung trực của YT hay N' thuộc ID.
Theo bổ đề thì AM, EF, ID đồng quy tại N nên [TEX]N \equiv N'[/TEX]. Từ đó Z,N,T thẳng hàng.
Ta có [TEX](AN,XY)=-1 \Rightarrow Z(AN,XY)=-1 \Rightarrow (JT,XY)=-1[/TEX] hay JXTY là tứ giác điều hòa.
Hình đính kèm:

Nếu có gì thắc mắc bạn có thể hỏi tại đây, chúng mình luôn sẵn sàng giúp đỡ.
Bạn có thể tham khảo thêm các kiến thức môn học khác tại đây.