[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
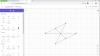
1, Cho M là trung điểm của đoạn thẳng AB. Trên cùng một nửa mặt phẳng bờ AB, ta vẽ các đoạn thẳng MC, MD sao cho góc AMC = BMD và MC = MD. CM
a, AC = BD
b, tam giác CAB = tam giác DBA
2, Cho tam giác ABC = tam giác A'B'C'. Trên cạnh BC lấy điểm M, trên cạnh B'C' lấy điểm M' sao cho BM = [tex]\frac{1}{3}[/tex] BC, C'M' = [tex]\frac{2}{3}[/tex] B'C'. Chứng minh rằng AM = A'M'
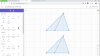
3, Cho tam giác ABC vuông tại A. Trên tia đối của tia AC lấy điểm D sao cho AD = AC
a, CM BA là phân giác của tam giác BCD
b, Trên tia đối của tia BA lấy điểm M. CM tam giác MBD = tam giác MBC
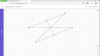
4, Vẽ hai đường thẳng AB và CD cắt nhau tại trung điểm O của mỗi đoạn thẳng đó. Gọi M và N lần lượt là trung điểm của AD và BC. CM:
a, OM = ON
b, Ba điểm M,O,N thẳng hàng
p/s: vẽ hình luôn nha mấy pạn
a, AC = BD
b, tam giác CAB = tam giác DBA
2, Cho tam giác ABC = tam giác A'B'C'. Trên cạnh BC lấy điểm M, trên cạnh B'C' lấy điểm M' sao cho BM = [tex]\frac{1}{3}[/tex] BC, C'M' = [tex]\frac{2}{3}[/tex] B'C'. Chứng minh rằng AM = A'M'
3, Cho tam giác ABC vuông tại A. Trên tia đối của tia AC lấy điểm D sao cho AD = AC
a, CM BA là phân giác của tam giác BCD
b, Trên tia đối của tia BA lấy điểm M. CM tam giác MBD = tam giác MBC
4, Vẽ hai đường thẳng AB và CD cắt nhau tại trung điểm O của mỗi đoạn thẳng đó. Gọi M và N lần lượt là trung điểm của AD và BC. CM:
a, OM = ON
b, Ba điểm M,O,N thẳng hàng
p/s: vẽ hình luôn nha mấy pạn