cho tam giác ABC,Â=60 độ.trực tâm H.Gọi M là điểm đối xứng với H qua BC
a)C/m:tam giác BHC=tam giác BMC
b)Tính góc BMC
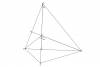
$a)$ $AH$ cắt $BC$ tại $D$ $\Rightarrow$ $AD$ là đường cao của $\Delta ABC$ $($trực tâm$)$ $\Rightarrow AH \bot BC$ tại $D$ $(1)$
$M$ đối xứng với $H$ qua $BC$ $\Rightarrow HM \bot BC$ và $BH=BM,CH=CM$ $(2)$
$(1)(2) \Rightarrow A,H,D,M$ thẳng hàng
$\Delta HBC = \Delta MBC$ $(c-c-c)$ $(đpcm)$ do $BC$ là cạnh chung $;$ $BH=BM (cmt)$ $;$ $CH=CM (cmt)$
$\Rightarrow \widehat {BMC}=\widehat {BHC}$ $(yttứ)$
$b)$ Tương tự $:$ $CH$ cắt $AB$ ở $E$ $\Rightarrow CE\bot AB$ ở $E$ $\Rightarrow \widehat {ECB}=\widehat {BAD}$ $($cùng phụ $\widehat {ABC}$$)$ hay $\widehat {HCD}=\widehat {BAD}$
Ta có $:$ $\Delta HDC \backsim \Delta BDA$ $(g-g)$ do $\widehat {HDC}=90^{\circ }=\widehat {BDA}$ $;$ $\widehat {HCD}=\widehat {BAD}$ $(cmt)$
$\Rightarrow \widehat {DHC}=\widehat {DBA}$ $(yttứ)$$.$ Chứng minh tương tự$,$ ta có $:$ $\widehat {DHB}=\widehat {BCA}$
Khi đó$,$ ta có $:$ $\widehat {BMC}=\widehat {BHC}=\widehat {BHD}+\widehat {DHB}=\widehat {ABC}+\widehat {ACB}=180^{\circ}-\widehat {BAC}=180^{\circ}-60^{\circ}=120^{\circ}$
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
