[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
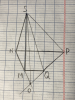
Trong mp(p) cho hình thang MNPQ đáy lớn NP. Lấy điểm s nằm ngoài mp(p) .Tìm giao tuyến 2 mp
A) (SMP) và (SNQ)
B) (SMN) và (SPQ)
A) (SMP) và (SNQ)
B) (SMN) và (SPQ)