Toán 7 $\triangle ABC, M$ là trung điểm $BC,...$ CM $DE=2AM, AM\perp DE$

[haianhchunguyen]

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

cho tam giác ABC, M là trung điểm của BC. Trên nửa mặt phẳng ko chứa C có bờ AB, vẽ Ax vuông góc vs AB, trên Ax lấy D sao cho AD=AB. Trên nửa mặt phẳng ko chứa B có bờ AC, vẽ Ay vuông góc vs AC, trên Ay lấy E sao cho AE=AC. CM:
a)DE=2AM
b)AM vuông góc DE

 

[Blue Plus]

a.
Trên tia đối của $MA$ lấy $K$ sao cho $KM=AM$
Nối $KC$
$\triangle ABM=\triangle KCM\Rightarrow AB=KC$
$\triangle ACK=\triangle EAD$
$\Rightarrow AK=ED$
mà $AK=KM+AM=2AM$
$\Rightarrow ED=2AM$
b.
Gọi $H$ là giao điểm của $AM$ và $DE$
$\widehat{MAH}=\widehat{MAB}+\widehat{BAD}+\widehat{DAH}$
$180^o=\widehat{MAB}+90^o+\widehat{DAH}$
$\widehat{MAB}+\widehat{DAH}=90^o$
Lại có:
$\widehat{AKC}=\widehat{ADE}(\triangle ACK=\triangle ECD)$
và $\widehat{AKC}=\widehat{BAM}(\triangle ABM=\triangle KCM)$
$\Rightarrow \widehat{ADE}=\widehat{BAM}$
$\Rightarrow \widehat{ADE}+\widehat{DAH}=\widehat{BAM}+\widehat{ADH}=90^o$
Xét $\triangle ADH$ ta có: $\widehat{ADE}+\widehat{DAH}+\widehat{AHD}=180^o\\\Rightarrow \widehat{AHD}=90^o\Rightarrow AM\perp DE$

 

[Vũ Lan Anh]

a.
Trên tia đối của $MA$ lấy $K$ sao cho $KM=AM$
Nối $KC$
$\triangle ABM=\triangle KCM\Rightarrow AB=KC$
$\triangle ACK=\triangle ECD$
$\Rightarrow AK=ED$
mà $AK=KM+AM=2AM$
$\Rightarrow ED=2AM$
b.
Gọi $H$ là giao điểm của $AM$ và $DE$
$\widehat{MAH}=\widehat{MAB}+\widehat{BAD}+\widehat{DAH}$
$180^o=\widehat{MAB}+90^o+\widehat{DAH}$
$\widehat{MAB}+\widehat{DAH}=90^o$
Lại có:
$\widehat{AKC}=\widehat{ADE}(\triangle ACK=\triangle ECD)$
và $\widehat{AKC}=\widehat{BAM}(\triangle ABM=\triangle KCM)$
$\Rightarrow \widehat{ADE}=\widehat{BAM}$
$\Rightarrow \widehat{ADE}+\widehat{DAH}=\widehat{BAM}+\widehat{ADH}=90^o$
Xét $\triangle ADH$ ta có: $\widehat{ADE}+\widehat{DAH}+\widehat{AHD}=180^o\\\Rightarrow \widehat{AHD}=90^o\Rightarrow AM\perp DE$

sai rồi
$\triangle ACK=\triangle ECD$ ????????
làm như này nha
\
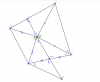
a, Trên tia đối Am lấy MK sao cho MK=MA
Xét [tex]\Delta AMC và \Delta BMK[/tex]
có: AM=MK
BM=MC
[tex]\widehat{M1}=\widehat{M2}[/tex] (đối đỉnh)
=> [tex]\Delta AMC = \Delta BMK[/tex]=>
[tex]\widehat{B2}=\widehat{C1}[/tex]
[tex]\widehat{C1}+\widehat{B1}=180^{\circ}- \widehat{BAC}[/tex] => [tex]\widehat{B2}+\widehat{B1}=180^{\circ}- \widehat{BAC[/tex]
= [tex]\widehat{DAE}[/tex](1)
**AC=BK
mà AC=AE(gt)=> AE=BK(2)
Ta có: AD=AB(gt)(3)
Từ(1)(2)(3) suy ra [tex]\Delta ABK= \Delta DAE[/tex]
=>DE=AK
mà AK=2AM=> DE=2Am(đpcm)
b, kéo dài AM cắt DE tại H (H thuộc DE)
Vì [tex]\Delta ABK= \Delta DAE[/tex]
nên[tex]\widehat{HDA}=\widehat{A2}[/tex]
mà:
[tex]\widehat{A1}+\widehat{A2}=90^{\circ} =>\widehat{HDA}+\widehat{A1}=90^{\circ} =>\widehat{DHA}=90^{\circ} [/tex]
=> AH vuông góc với DE hay AM vuông góc với DE(đpcm)

 

[haianhchunguyen]

a.
Trên tia đối của $MA$ lấy $K$ sao cho $KM=AM$
Nối $KC$
$\triangle ABM=\triangle KCM\Rightarrow AB=KC$
$\triangle ACK=\triangle EAD$
$\Rightarrow AK=ED$
mà $AK=KM+AM=2AM$
$\Rightarrow ED=2AM$
b.
Gọi $H$ là giao điểm của $AM$ và $DE$
$\widehat{MAH}=\widehat{MAB}+\widehat{BAD}+\widehat{DAH}$
$180^o=\widehat{MAB}+90^o+\widehat{DAH}$
$\widehat{MAB}+\widehat{DAH}=90^o$
Lại có:
$\widehat{AKC}=\widehat{ADE}(\triangle ACK=\triangle ECD)$
và $\widehat{AKC}=\widehat{BAM}(\triangle ABM=\triangle KCM)$
$\Rightarrow \widehat{ADE}=\widehat{BAM}$
$\Rightarrow \widehat{ADE}+\widehat{DAH}=\widehat{BAM}+\widehat{ADH}=90^o$
Xét $\triangle ADH$ ta có: $\widehat{ADE}+\widehat{DAH}+\widehat{AHD}=180^o\\\Rightarrow \widehat{AHD}=90^o\Rightarrow AM\perp DE$

sao tam giác ACK= tam giác AED vậy