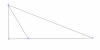
Hạ BH vuông góc với AC. Do A là góc tù nên H nằm ngoài đoạn AC.
BAH và BAC là hai góc kề bù nên [tex]\widehat{BAH}+\widehat{BAC}=180^{\circ}\\ \Rightarrow \widehat{BAH}=180^{\circ}-\widehat{BAC}\\ \Rightarrow \widehat{BAH}=180^{\circ}-120^{\circ}\\ \Rightarrow \widehat{BAH}=60^{\circ}[/tex]
Xét tam giác AHB vuông tại H
[tex]\Rightarrow AH=AB.\cos BAH=AB.\cos 60^{\circ}=3.\frac{1}{2}=1,5;\\ BH=AB.\sin BAH=AB.\sin 60^{\circ}=3.\frac{\sqrt{3}}{2}=\frac{3\sqrt{3}}{2}[/tex]
Ta có: [tex]CH=AH+AC=1,5+5=6,5[/tex]
Áp dụng định lý Pytago trong tam giác BHC vuông tại H ta có:
[tex]BH^{2}+HC^{2}=BC^{2}\\ \Rightarrow (\frac{3\sqrt{3}}{2})^2+6,5^{2}=BC^{2}\\ \Rightarrow BC^{2}=49\\ \Rightarrow BC=7.[/tex]
{Kiến thức bạn trên sử dụng là định lý Cosin nha, được học chính thức ở chương trình lớp 10, đối với kiến thức cơ bản lớp 9 thì không được giới thiệu}
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
