Toán Toán khó

[Victoriquedeblois]

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

Bài 1 ( 2,0 điểm) Cho biểu thức
P=[tex]\frac{15\sqrt{x}-11}{x+2\sqrt{x}-3}+\frac{3\sqrt{x}-2}{1-\sqrt{x}}-\frac{2\sqrt{x}+3}{\sqrt{x}+3} (x\geq 0,x\neq1)[/tex]
a. Rút gọn biểu thức P
b. Tìm x để P< [tex]\frac{1}{2}[/tex]
Bài 2( 2.0 điểm)
a. Cho phương trình [tex]x^{2}-(2m-1)x+m^{2}-m-6=0[/tex] ( m là tham số). Tìm m để phương trình có hai nghiệm phân biệt x1,x2 sao cho -5<x1<x2<5
b. Cho n là số nguyên dương và các số
A= 44...44(2n chữ số4), B=88...88 ( n chữ số 8) Cmr: A+2B+4 là số chính phương
Bài 3(2.0 điểm)
a. Để thành lập đội tuyển học sinh gỏi khối 9 ở một trường THCS, nhà trường tổ chức cho 111 học sinh tham gia thi chọn đội tuyển ở các môn Toán, Văn, Ngoại Ngữ. Kết quả có 70 học sinh giỏi Toán, 65 học sinh giỏi văn, 62 học sinh giỏi Ngoại Ngữ trong đó có 49 học sinh giỏi cả Toán và Văn, 32 học sinh giỏi cả Toán và Ngoại Ngữ, 34 học sinh giỏi cả Văn và Ngoại Ngữ, 6 học sinh không đạt yêu cầu bất cứ món nào trong ba môn. Hỏi có bao nhiêu học sinh giỏi cả ba môn Toán, Văn, Ngoại Ngữ?
b. Giải hệ phương trình:
[tex]\left\{\begin{matrix} x=y^{3}-5y^{2}+8y-3 & & \\ y=-2x^{2}+10x^{2}-16x+9& & \end{matrix}\right.[/tex]
Bài 4(0.5 điểm) Chờ a, b, c là các số thực dương thỏa mãn [tex]a^{2}+ 2b^{2}+3c^{2}=1[/tex]
Tìm giá trị nhỏ nhất của biểu thức P= [tex]2a^{3}+3b^{3}+4c^{3}[/tex]
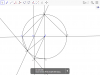
Bài 5(3,5 điểm) Cho đường tròn (O;R) có hai đường kính AB và CD vuông góc với nhau. Trên đoạn AB lấy điểm M( M không trùng O và hai đầu mút A,B). Đường thẳng CM cắt đường tròn (O) tại điểm thứ hai là N. Đường thẳng vuông góc với AB tại M cắt tiếp tuyến tại N của đường tròn (O) tải P. Chứng minh rằng :
a. Tứ giác OMNP là tứ giác nội tiếp
b. Tứ giác CMPO là hình bình hành và tích CM.CN không đổi
c. Khi M di chuyển trên đoạn AB thì điểm P chạy trên một đoạn thẳng cố định

 

[♫ Phạm Công Thành ♫]

2b,
A+2B+4
=4.111...1+2.8.111...1+4
=4.[tex]\frac{10^{2n}-1}{9}[/tex] +2.8.[tex]\frac{10^{n}-1}{9}+4[/tex]
= [tex]\frac{4.10^{2n}-4}{9}+\frac{16.10^{n}-16}{9}+\frac{36}{9}[/tex]
[tex]=\frac{(2.10^{n})^{2}+2.2.10^{n}.4+16}{9}[/tex]
[tex]=\frac{(2.10^{n}+4)^{2}}{9}[/tex]
[tex]=(\frac{2.10^{n}+4}{3})^{2}[/tex]
Mà [tex]\frac{2.10^{n}+4}{3}[/tex] nguyên (tổng các chữ số bằng 6 chia hết cho 3)
=>A+2B+4 là số chính phương

 

[Thần mộ 2]

Câu bất
Áp dụng Holder thì có lẽ ngắn hơn một chút,tuy nhiên lại phải chứng minh do BĐT này không được học ở THCS(._.)
Thành ra cũng vẫn dài.
Em làm cách này,bác tham khảo
Giả định:$a=x,b=y,c=z$
Ta có:
$2(a^3+a^3+x^3)\geq 6xa^2$
$3(b^3+b^3+y^3)\geq 9yb^2$
$4(c^3+c^3+z^3)\geq 12zc^2$
Cộng vế theo vế:
$2P+2x^3+3y^3+4z^3\geq 6xa^2+9yb^2+12zc^2$
Có hệ:
$\left\{\begin{matrix} &\frac{6x}{1}=\dfrac{9y}{2}=\dfrac{12z}{3} \\ &x^2+2y^2+3z^2=1 \end{matrix}\right.$
$\Leftrightarrow \left\{\begin{matrix} &x=\frac{6}{\sqrt{407}} & \\ &y=\frac{8}{\sqrt{407}} & \\ &z=\frac{9}{\sqrt{407}} & \end{matrix}\right.$
$\Rightarrow P\geq \frac{12}{\sqrt{407}}$
Cái phần dấu bằng tự giải nhé.Rắc rối quá.

 

[Nguyễn Xuân Hiếu]

Câu hình:
a)$\widehat{PMO}=\widehat{ONP}=90^0$.
Do đó tứ giác $NMOP$ nt.
b)Theo đề bài dễ thấy $PM//OC$.
Mặt khác: $\widehat{MNO}=\widehat{MCO}=\widehat{NMP}$.
Mà tứ giác $NMOP$ nt. Do đó $NMOP$ là hình thang cân.
Do đó $NM//OP$.
Kết hợp 2 cái // do đó $CMPO$ nt.
Ta có: $\widehat{CAM}=\widehat{CBA}=\widehat{CNA}$.
Do đó $\triangle CAM \sim \triangle CNA \Rightarrow CM.CN=CA^2=const$.
c)Từ câu b) chứng minh $PD$ là tiếp tuyến.
Do dó $P$ di chuyển trên một đường thẳng song song với $AB$ và cố định một khoảng bằng $OD=R$.