Toán 8 Tổng hợp hình học

[Cao Khắc Bảo Sơn]

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

 

[Tungtom]

Mình vẽ hình theo thứ tự các câu nha bạn:
a)
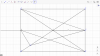
Câu a bạn chỉ cần chứng minh tam giác NCD= tam giác MAB theo trường hợp cạnh góc cạnh.
=> [tex]\widehat{DNC}[/tex]=[tex]\widehat{BMA}[/tex]( 2 góc tương ứng.
Ta có:[tex]\widehat{DNC}+\widehat{CNM}=90^o[/tex].
[tex]\widehat{BMA}+\widehat{AMN}=90^0[/tex] .
Mà [tex]\widehat{DNC}[/tex]=[tex]\widehat{BMA}[/tex] => [tex]\widehat{CNM}[/tex]=[tex]\widehat{AMN}[/tex].
Mà đây là hai góc nằm ở vị trí so le trong
=> AM // NC.
Vì ABCD là hình chữ nhật nên AC=BD.
=> [tex]\frac{AC}{2}=\frac{BD}{2}[/tex]=> AO=OD=>[tex]\Delta AOD[/tex] cân tại O(1)
Bạn có thể tự chứng minh được N là trung điểm của AD=> ON là đường trung tuyến của [tex]\Delta AOD[/tex](2)
Từ (1) và (2)=> ON cũng là đường phân giác của tam giác AOD( tính chất của tam giác cân)
=>[tex]\widehat{AON}=\widehat{NOD}[/tex] hay [tex]\widehat{AON}=\widehat{NOH}[/tex].
Chứng minh được: [tex]\Delta AON\sim \Delta NOH[/tex] theo trường hợp góc-góc.
=>[tex]\frac{AN}{NH}[/tex]=[tex]\frac{AO}{NO}[/tex].(3) và [tex]\widehat{NAO}=\widehat{HNO}[/tex].
Bạn tự chứng minh được NO= OM=> 2NO=NM=>[tex]\frac{AC}{NM}[/tex]=[tex]\frac{2AO}{2NO}=\frac{AO}{NO}[/tex].(4)
Từ (3) và (4)=>[tex]\frac{AN}{NH}[/tex]=[tex]\frac{AC}{NM}[/tex].(5)
Vì [tex]\widehat{NAO}=\widehat{HNO}[/tex] hay [tex]\widehat{NAC}=\widehat{HNM}[/tex](6)
Từ (5) và (6) có thể chứng minh [tex]\Delta HNM[/tex]~[tex]\Delta NAC[/tex] theo trường hợp cặp cạnh tỉ lệ và góc xen giữa bằng nhau.
=>[tex]\widehat{HMN}[/tex]=[tex]\widehat{NCA}[/tex]
Mà [tex]\widehat{NCA}=\widehat{MAC}[/tex]( 2 góc so le trong)=>[tex]\widehat{HMN}=\widehat{MAC}[/tex](đpcm)
Mình mới làm câu a vì mình chưa đủ thời gian, sớm nhất là ngày mai mình sẽ bổ sung thêm phần còn lại nha. Nếu chỗ nào bạn chưa hiểu hoặc mình gõ sai thì hãy chỉ ra cho mình nha, cảm ơn bạn nhiều.

 

[shorlochomevn@gmail.com]

b, +, có: tam giác HNM đồng dạng tam giác NAC (câu a) => AN/AC= HN/MN
=> AN/AO= HN/OM => AN/NH= AO/OM
lại có: góc DNH=góc AON (cùng phụ góc OAD)
=> tam giác ANH đồng dạng tam giác AOM
=> góc AHN=góc AMO=góc ONC
=> góc AHN+góc 90= góc ONC+90
=> góc DHA=góc ANC
lại có: góc NAC=góc ADH
=> tam giác ANC đồng dạng tam giác DHA (g.g)
=> AN/AC= DH/AD => AN.BC=DH.AC
+, có: góc AON=góc HON (tự cm)
=> 180- góc AON=180- góc HON
=> góc AOM= góc MOH
mặt khác góc OAM=góc OMH (câu a)
=> tam giác AOM đồng dạng tam giác MOH (g.g)
=> góc OHM=góc OMA=góc AHN
=> góc OHM+ góc OHA=góc AHN+góc OHA=góc OHN=90
=> góc MHA=90
=> đpcm
c, có: IA.IB+ AK.KD= DT.BT
<=> IA.IB + AK.KD= (BD-BT).BT
<=> IA.IB + AK.KD= BD.BT- (IB^2 + AK^2)
<=> IB.AB + AK.AD=BD.BT
có: tam giác BIT đồng dạng tam giác BAD (g.g)
=> [tex]\frac{BI}{AB}=\frac{IT}{AD}=\frac{BT}{BD}\\\\ <=> \frac{BI.AB}{AB^2}=\frac{AK.AD}{AD^2}=\frac{BT.BD}{BD^2}\\\\=\frac{BI.AB+AK.AD}{AB^2+AD^2}=\frac{BI.AB+AK.AD}{BD^2}\\\\ => ĐPCM[/tex]
d, mình chưa nghĩ ra...giờ muộn rồi....

 

[iceghost]

d/ Hạ $TS \perp MN$. Mục tiêu của mình là $\triangle{TSN} \sim \triangle{NDE}$ hay $\dfrac{TS}{ND} = \dfrac{SN}{DE} \ (1)$
Ta có $$\dfrac{TS}{ND} = \dfrac{TS}{BM} = \dfrac{OS}{OM}$$
và $$\dfrac{OM}{DE} = \dfrac{TO}{TD} = \dfrac{SO}{SN}$$
Từ đó suy ra $\dfrac{SN}{DE} = \dfrac{OS}{OM} = \dfrac{TS}{ND}$
Vậy $\triangle{TSN} \sim \triangle{NDE}$ nên $\widehat{TNM} = \widehat{NED} = \widehat{MNE}$. Đpcm!