[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
 Đây sẽ là một series dài để chia sẻ các mô hình bài toán mà học sinh lớp 8 sẽ thường gặp. Các bạn hãy cùng theo dõi chủ để đề cập nhập nhanh nhất những bài này nha.
Đây sẽ là một series dài để chia sẻ các mô hình bài toán mà học sinh lớp 8 sẽ thường gặp. Các bạn hãy cùng theo dõi chủ để đề cập nhập nhanh nhất những bài này nha.CÁC BÀI TOÁN HÌNH HỌC 8 THƯỜNG GẶP
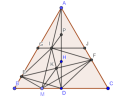
Bài toán 1: Cho tam giác [imath]ABC[/imath] vuông ở [imath]A[/imath], đường cao [imath]AH[/imath]. Kẻ [imath]HD, HE[/imath] lần lượt vuông góc với [imath]AB, AC[/imath] [imath](D\in AB[/imath], [imath]E\in AC)[/imath]. Gọi [imath]O[/imath] là giao điểm của [imath]AH[/imath] và [imath]DE[/imath].
1) Chứng minh [imath]ADHE[/imath] là hình chữ nhật
2) Chứng minh [imath]AE.AC=AD.AB[/imath]
3) Kẻ tia [imath]Ax\bot DE[/imath] cắt BC tại M. Chứng minh M là trung điểm BC
4) Gọi [imath]P,Q[/imath] lần lượt là trung điểm của [imath]BH,HC[/imath]. Tứ giác [imath]DPQE[/imath] là hình gì?
5) Chứng minh [imath]O[/imath] là trực tâm của [imath]\Delta ABQ[/imath]
6) Chứng minh [imath]S_{ABC}=2S_{DPQE}[/imath]
7) Tam giác ABC cần thêm điều kiện gì để [imath]DE=2EQ[/imath]
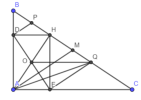
1) Chứng minh [imath]ADHE[/imath] là hình chữ nhật (hoặc chứng minh [imath]AH=DE)[/imath]
Xét tứ giác [imath]ADHE[/imath] có [imath]\widehat{DAE}=\widehat{ADH}=\widehat{HEA}=90^\circ[/imath]
[imath]\Rightarrow ADHE[/imath] là hình chữ nhật [imath]\Rightarrow AH=DE[/imath]
2) Chứng minh [imath]AE.AC=AD.AB[/imath] (hoặc chứng minh [imath]\widehat{AEB}=\widehat{ACD})[/imath]
[imath]ADHE[/imath] là hình chữ nhật [imath]\Rightarrow \widehat{AED}=\widehat{AHD}[/imath]
Mà [imath]\widehat{AHD}=\widehat{ABC}[/imath] (cùng phụ với [imath]\widehat{DHB}[/imath])
Xét [imath]\Delta ADE[/imath] và [imath]\Delta ACB[/imath] cùng vuông tại A
có [imath]\widehat{AED}=\widehat{ABC}[/imath]
[imath]\Rightarrow \Delta ADE\sim \Delta ACB[/imath]
[imath]\Rightarrow \dfrac{AD}{AC}=\dfrac{AE}{AB}\Rightarrow AB.AD=AC.AE[/imath]
Để chứng minh ý trong ngoặc cần chứng minh thêm [imath]\Delta ABE\sim \Delta ACD[/imath]
3) Kẻ tia [imath]Ax\bot DE[/imath] cắt BC tại M. Chứng minh M là trung điểm BC (hoặc M là trung điểm BC chứng minh [imath]AM\bot DE)[/imath]
Ta có: [imath]\widehat{MAE}=\widehat{ADE}[/imath] (cùng phụ với [imath]\widehat{AED}[/imath])
[imath]\widehat{ADE}=\widehat{ACB} (\Delta ADE\sim \Delta ACB)[/imath]
Suy ra [imath]\widehat{MAC}=\widehat{MCA}\Rightarrow \Delta AMC[/imath] cân tại M [imath]\Rightarrow MA=MC[/imath]
Chứng minh tương tự ta có: [imath]MA=MB[/imath]
Suy ra [imath]MA=MB\Rightarrow M[/imath] là trung điểm của AB.
4) Gọi [imath]P,Q[/imath] lần lượt là trung điểm của [imath]BH,HC[/imath]. Tứ giác [imath]DPQE[/imath] là hình gì? (hoặc chứng minh [imath]\Delta DEQ[/imath] là tam giác vuông)
Xét [imath]\Delta ABH[/imath] vuông tại H và [imath]\Delta CBA[/imath] vuông tại A
có [imath]\widehat{ABC}[/imath] chung
[imath]\Rightarrow \Delta ABH\sim \Delta CBA[/imath]
[imath]\Rightarrow \widehat{BAH}=\widehat{ACB}[/imath]
Mà [imath]\widehat{BAH}=\widehat{DEH}[/imath] (ADHE là hình chữ nhật)
Suy ra [imath]\widehat{DEH}=\widehat{ACB}[/imath]
Xét [imath]\Delta HEC[/imath] vuông tại E có EQ là đường trung tuyến
[imath]\Rightarrow QE=HQ\Rightarrow \Delta EQH[/imath] cân tại Q[imath]\Rightarrow \widehat{QEH}=\widehat{QHE}[/imath]
Ta có: [imath]\widehat{DEQ}=\widehat{DEH}+\widehat{HEQ}=\widehat{ACB}+\widehat{EHQ}=180^\circ-\widehat{HEC}=90^\circ[/imath]
[imath]\Rightarrow DE\bot EQ[/imath]
Chứng minh tương tự ta có: [imath]DP\bot DE[/imath]
Suy ra tứ giác [imath]DPQE[/imath] là hình thang vuông
5) Chứng minh [imath]O[/imath] là trực tâm của [imath]\Delta ABQ[/imath] (hoặc chứng minh [imath]BO\bot AQ)[/imath]
Ta có: [imath]ADHE[/imath] là hình chữ nhật, [imath]O=AH\cap DE[/imath]
[imath]\Rightarrow O[/imath] là trung điểm của [imath]AH,DE[/imath]
Xét [imath]\Delta AHC[/imath] có [imath]O,Q[/imath] lần lượt là trung điểm của [imath]HA,HC[/imath]
[imath]\Rightarrow OQ[/imath] là đường trung bình
[imath]\Rightarrow OQ//AC\Rightarrow OQ\bot AB (AB\bot AC)[/imath]
Mà [imath]AO\bot BQ[/imath]
Suy ra [imath]O[/imath] là trực tâm của [imath]\Delta ABQ[/imath]
6) Chứng minh [imath]S_{ABC}=2S_{DPQE}[/imath]
[imath]\dfrac{S_{EQH}}{S_{EHC}}=\dfrac{QH}{HC}=\dfrac{1}2\Rightarrow S_{EQH}=\dfrac{1}2S_{HEC}[/imath]
Tương tự ta có: [imath]S_{DPH}=\dfrac{1}2S_{DBH}[/imath]
[imath]S_{DHE}=\dfrac{1}2DH.HE=\dfrac{1}2S_{ADHE}[/imath]
[imath]S_{DPQE}=S_{DPH}+S_{DHE}+S_{HED}=\dfrac{1}2S_{DBH}+\dfrac{1}2S_{ADHE}+\dfrac{1}2S_{HEC}=\dfrac{1}2S_{ABC}\Rightarrow S_{ABC}=2S_{DPQE}[/imath]
7) Tam giác ABC cần thêm điều kiện gì để [imath]DE=2EQ[/imath]
[imath]DE=2OE=2EQ\Rightarrow OE=EQ\Rightarrow \Delta OEQ[/imath] vuông cân tại [imath]E[/imath]
[imath]\Rightarrow \widehat{EQO}=45^\circ\Rightarrow \widehat{QEC}=45^\circ (OQ//AC)[/imath]
[imath]\Rightarrow \widehat{ECQ}=45^\circ\Rightarrow \Delta ABC[/imath] vuông cân tại [imath]A[/imath]
Vậy cần thêm điều kiện [imath]AB=AC[/imath] để [imath]DE=2EQ[/imath]
Các bạn còn ý nào liên quan tới mô hình này, hãy trả lời phía dưới này để được giải đáp nhé <3
Last edited:


 Hai bài toán tiếp theo đây các em sẽ dễ gặp trong phần hình vuông nha.
Hai bài toán tiếp theo đây các em sẽ dễ gặp trong phần hình vuông nha.