P
pe_quy_toc
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Dạng 1: Tìm giao điểm
a, d1 giao d2 tại A
chỉ ra mp chứa d1, d2 rồi mới chỉ ra quan hệ d1, d2
b, d giao mp(P) tại M
B1: Tìn mp(Q) chứa đường d1 và 1 đường trong (P) ( mp(Q) thường là tam giác có 1 cạch là d)
B2: trong (Q) d cắt d1 trong (P) => d giao (P)
Dạng 2: C/m 3 điểm thẳng hàng hoặc tìm quỹ tích 1 điểm
- C/m 3 điểm này là điểm chung của 2 mp để kết luận 3 điểm này nằm trên giao tuyến của 2 mp nên chúng thẳng hàng
- tìm quỹ tích cũng tương tự
Dạng 3: C/m 3 đường đồng qui
Dựa vào định lí: d1, d2, d3 là 3 giao tuyến của 3 mp phân biệt, bác bỏ khả năng song song
Dạng 4: Cách tính góc giữa 2 đường thẳng
Cách 1 : dùng 2 vectơ chỉ phương của d1 và d2. Sau đó tính cos của 2 vec tơ này bằng trị tuyệt đối của tích vô hướng trên tích độ dài
được dùng khi có tọa độ
Cách 2: Dồn góc vào 1 tam giác rồi tính 3 cạch của tam giác đó, sau đó dùng định lí cos để tính góc
Dạng 5: Xác định góc giữa đường thẳng và mặt phẳng
B1: chỉ ra đường vuông góc AH hạ từ A thuộc d xuống (P)
B2: chỉ ra hình chiếu HB của d trên (P)
B3: góc ABH= g(d,(P))=
,
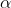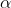thuộc khoảng (0;90)
Dạng 6: Xác định góc giữa 2 mp
B1: Xác định đường vuông góc SH
B2: từ chân H tìm ( không có) thì vẽ HK vuông góc với giao tuyến d1
B3: Dùng định lí 3 đường vuông góc chỉ ra SK vuông góc với d1
B4: kết luận góc SKH= g((P),(Q))
Dạng 7: Khoảng cách giữa 2 đường thẳng chéo nhau
B1: Tìm 1 mp(P) chứa d1//d2 (d1 thuộc (P); d2 không thuộc (P))
B2: tìm trên đường d2 hoặc chọn trên đường d2: 1 điểm M mà dễ xác định MH vuông góc với (P)
B3: Tính MH và MH=d(d1,d2)
Đặc biệt chú ý: Xác định đường cao của hình chóp trong một số trường hợp
1, có 1 trong 3 giả thiết sau
a, Chóp đều
b, Chóp có cạch bên bằng nhau
c, chóp có cạch bên nghiêng trên đáy 1 góc
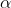
=> Đường cao SO đi qua tâm O đường tròn ngoại tiếp đáy
2, Hình chóp có 2 mặt cùng vuông với đáy thì đường ccao SO chính là giao tuyến của 2 mặt bên này
3, Chóp có 1 mặt bên vuông với đáy thì đường cao hình chóp chính là đường cao của mặt bên này.( t/c 2 mp vuông góc)
4,Hình chóp có các mặt bên nghiêng trên đáy 1 góc
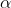thì đường cao của hình chóp đi qua tâm đường tròn nội tiếp đáy
5, Hình chóp có 2 mặt tạo với đáy 1 góc
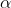thì đường cao SO có điểm O nằm trên đường phân giác tạo bởi 2 cạch đáy của 2 mặt bên đó
a, d1 giao d2 tại A
chỉ ra mp chứa d1, d2 rồi mới chỉ ra quan hệ d1, d2
b, d giao mp(P) tại M
B1: Tìn mp(Q) chứa đường d1 và 1 đường trong (P) ( mp(Q) thường là tam giác có 1 cạch là d)
B2: trong (Q) d cắt d1 trong (P) => d giao (P)
Dạng 2: C/m 3 điểm thẳng hàng hoặc tìm quỹ tích 1 điểm
- C/m 3 điểm này là điểm chung của 2 mp để kết luận 3 điểm này nằm trên giao tuyến của 2 mp nên chúng thẳng hàng
- tìm quỹ tích cũng tương tự
Dạng 3: C/m 3 đường đồng qui
Dựa vào định lí: d1, d2, d3 là 3 giao tuyến của 3 mp phân biệt, bác bỏ khả năng song song
Dạng 4: Cách tính góc giữa 2 đường thẳng
Cách 1 : dùng 2 vectơ chỉ phương của d1 và d2. Sau đó tính cos của 2 vec tơ này bằng trị tuyệt đối của tích vô hướng trên tích độ dài
được dùng khi có tọa độ
Cách 2: Dồn góc vào 1 tam giác rồi tính 3 cạch của tam giác đó, sau đó dùng định lí cos để tính góc
Dạng 5: Xác định góc giữa đường thẳng và mặt phẳng
B1: chỉ ra đường vuông góc AH hạ từ A thuộc d xuống (P)
B2: chỉ ra hình chiếu HB của d trên (P)
B3: góc ABH= g(d,(P))=
Dạng 6: Xác định góc giữa 2 mp
B1: Xác định đường vuông góc SH
B2: từ chân H tìm ( không có) thì vẽ HK vuông góc với giao tuyến d1
B3: Dùng định lí 3 đường vuông góc chỉ ra SK vuông góc với d1
B4: kết luận góc SKH= g((P),(Q))
Dạng 7: Khoảng cách giữa 2 đường thẳng chéo nhau
B1: Tìm 1 mp(P) chứa d1//d2 (d1 thuộc (P); d2 không thuộc (P))
B2: tìm trên đường d2 hoặc chọn trên đường d2: 1 điểm M mà dễ xác định MH vuông góc với (P)
B3: Tính MH và MH=d(d1,d2)
Đặc biệt chú ý: Xác định đường cao của hình chóp trong một số trường hợp
1, có 1 trong 3 giả thiết sau
a, Chóp đều
b, Chóp có cạch bên bằng nhau
c, chóp có cạch bên nghiêng trên đáy 1 góc
=> Đường cao SO đi qua tâm O đường tròn ngoại tiếp đáy
2, Hình chóp có 2 mặt cùng vuông với đáy thì đường ccao SO chính là giao tuyến của 2 mặt bên này
3, Chóp có 1 mặt bên vuông với đáy thì đường cao hình chóp chính là đường cao của mặt bên này.( t/c 2 mp vuông góc)
4,Hình chóp có các mặt bên nghiêng trên đáy 1 góc
5, Hình chóp có 2 mặt tạo với đáy 1 góc