R
rua_it
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
[tex]\mathrm{\blue{:\ \left{\begin{(a+b+c)^3=32abc}\\{\frac{383-165.\sqrt{5}}{2} \leq \frac{a^4+b^4+c^4}{(a+b+c)^4} \leq \frac{9}{128}[/tex]

[tex]\mathrm{\blue{\left{\begin{x,y \in\ [-3;2]: \ x^3+y^3=2}\\{\sqrt[3]{4} \leq x^2+y^2 \leq 4+\sqrt[3]{36}[/tex]
:khi (165):
[tex]\mathrm{\red{\left{\begin{1 \geq z \geq y>x>0}\\{3x+2y+z \leq 4}\\{3x^2+2y^2+z^2 \leq \frac{16}{3}[/tex]
:khi (54):
[tex]\mathrm{\red{\left{\begin{sinB=(\sqrt{2}-cosC).sinA}\\{sinC=(\sqrt{2}-cosB).sinA \\ \triangle ABC=?[/tex]
 [tex]\mathrm{\blue{x,y \in\ [-3;2][/tex]
[tex]\mathrm{\blue{x,y \in\ [-3;2][/tex] 
:khi (96):


[tex]\mathrm{\blue{\left{\begin{x,y \in\ (0;1):x+y=1}\\{ x^x+y^y \geq \sqrt{2}[/tex]
Sao có mỗi 2 ta nhỉ [tex]\ \mathrm{\red{bigbang195[/tex]
[tex]\mathrm{\blue{\left{\begin{x,y \in\ [-3;2]: \ x^3+y^3=2}\\{\sqrt[3]{4} \leq x^2+y^2 \leq 4+\sqrt[3]{36}[/tex]
:khi (165):
[tex]\mathrm{\red{\left{\begin{1 \geq z \geq y>x>0}\\{3x+2y+z \leq 4}\\{3x^2+2y^2+z^2 \leq \frac{16}{3}[/tex]
:khi (54):
[tex]\mathrm{\red{\left{\begin{sinB=(\sqrt{2}-cosC).sinA}\\{sinC=(\sqrt{2}-cosB).sinA \\ \triangle ABC=?[/tex]
Em làm tiếp đi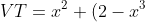^{\frac{2}{3}})
Xong tính đạo hàm ạ
.gif)
[tex]\mathrm{\red{Without \ loss \ of \ gererality \ we \ assume \ that \ a+b+c=4[/tex]Bài này chuyển r về p nhưng vẫn còn 2 biến thế có tìm được cực trị ko anh
.gif)
:khi (96):
[tex]\mathrm{\red{\left{\begin{f(t)=(2-t)^{\frac{2}{3}}+t^{\frac{2}{3}}}\\{ t \in\ [-6;8][/tex]Tìm được đỉnh rồi so sánh với f(-3) và f(2) ạ nhưng mà em ko biết tính đạo hàm cái có căn đâu ạ chỉ biếtthôi ạ'=2x)
)
:khi (117)::khi (117):
[tex]\mathrm{\blue{\left{\begin{x,y \in\ (0;1):x+y=1}\\{ x^x+y^y \geq \sqrt{2}[/tex]
Sao có mỗi 2 ta nhỉ [tex]\ \mathrm{\red{bigbang195[/tex]
Last edited by a moderator:

