 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
1) $3x+4y=5\Rightarrow y=\dfrac{5-3x}{4}$
bn cm theo kiểu này đc ko1) $3x+4y=5\Rightarrow y=\dfrac{5-3x}{4}$
$\Rightarrow x^2+y^2=x^2+\dfrac{(5-3x)^2}{16}=\dfrac{25x^2-30x+25}{16}=\dfrac{(25x^2-30x+9)+16}{16}=\dfrac{(5x-3)^2}{16}+1\geq 1$
Dấu '=' xảy ra khi $x=\dfrac 35;y=\dfrac 45$
2) Áp dụng BĐT Svac ta có:
$a^2+b^2+c^2\geq \dfrac{(a+b+c)^2}3=\dfrac 34$
Dấu '=' xảy ra khi $a=b=c=\dfrac12$
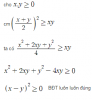 , ko cần tìm x ,y
, ko cần tìm x ,yý mh là bài 2 í có cách cm nào khác ko tại mh ch hc tối BDT này
bn cm theo kiểu này đc ko View attachment 16788, ko cần tìm x ,y
Nếu cm theo kiểu trên thì...^^ý mh là bài 2 í có cách cm nào khác ko tại mh ch hc tối BDT này
còn b1 thì sao bn mh bí quáNếu cm theo kiểu trên thì...^^
$a^2+b^2+c^2\geq \dfrac{(a+b+c)^2}{3}$
$\Leftrightarrow 3(a^2+b^2+c^2)\geq (a+b+c)^2$
$\Leftrightarrow 2a^2+2b^2+2c^2\geq 2ab+2bc+2ca$
$\Leftrightarrow (a^2-2ab+b^2)+(b^2-2bc+c^2)+(c^2-2ca+a^2)\geq 0$
$\Leftrightarrow (a-b)^2+(b-c)^2+(c-a)^2\geq 0$ (luôn đúng)
Áp dụng BĐT trên ta có đpcm
p/s: ko thì áp dụng BĐT Cô si vào cx đc, chắc bạn học rồi nhỉ? ^^.
bdt cô si đc hả bn , lm ntn zNếu cm theo kiểu trên thì...^^
$a^2+b^2+c^2\geq \dfrac{(a+b+c)^2}{3}$
$\Leftrightarrow 3(a^2+b^2+c^2)\geq (a+b+c)^2$
$\Leftrightarrow 2a^2+2b^2+2c^2\geq 2ab+2bc+2ca$
$\Leftrightarrow (a^2-2ab+b^2)+(b^2-2bc+c^2)+(c^2-2ca+a^2)\geq 0$
$\Leftrightarrow (a-b)^2+(b-c)^2+(c-a)^2\geq 0$ (luôn đúng)
Áp dụng BĐT trên ta có đpcm
p/s: ko thì áp dụng BĐT Cô si vào cx đc, chắc bạn học rồi nhỉ? ^^.
bài 1 chỉ thay vào thôi bạn vs lại cách tìm min đó cx học rồi mà ^^còn b1 thì sao bn mh bí quá
Áp dụng BĐT Cô si ta có:bdt cô si đc hả bn , lm ntn z

