Toán Toán khó

[Thoòng Quốc An]

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

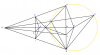
1. Cho đường tròn (O;R) và điểm M nằm ngoài đường tròn. Từ M kẻ hai tiếp tuyến MA,MB với đường tròn (O) (A,B là các tiếp điểm ) . Qua A vẽ dây song song với MB. Đường thẳng MD cắt đường tròn (O) tại C, gọi I là giao điểm của AC và BM
a) CM: Tứ giác MAOB nội tiếp và xác định tâm K của đường tròn đó
b) CM: Tam giác BAD cân
c) CM I là trung điểm BM
d) Gọi E là trung điểm MA, G là trọng tâm của tam giác MBE. CM: KG vuông góc với BE
câu c,d nha

 

[iceghost]

c) Dễ dàng CM được $\triangle{IBC} \sim \triangle{IAB}$ (g-g), suy ra $\dfrac{IB}{IA} = \dfrac{IC}{IB}$ hay $IB^2 = IA \cdot IC$
Ta sẽ CM $IM^2 = IA \cdot IC$. Thật vậy : $\widehat{IMC} = \widehat{ADC}$ (so le trong) và $\widehat{ADC} = \widehat{IAM}$ (góc nt = góc tạo bởi tia tiếp tuyến và dây cung cùng chắn một dây), suy ra $\widehat{IMC} = \widehat{IAM}$. Từ đây CM được $\triangle{IMC} \sim \triangle{IAM}$ (g-g), suy ra $\dfrac{IM}{IA} = \dfrac{IC}{IM}$ hay $IM^2 = IA \cdot IC$
Khi đó $IB^2 = IM^2$ hay $IB = IM$, ta thu được đpcm
d) Mình không biết là liệu có cách khác không, nhưng bạn thử tham thảo cách này. Mình chỉ vạch ra hướng đi thôi nhé
Gọi $J$ là giao điểm của tia $MG$ và $AB$, $H$ là giao điểm của $MO$ và $AB$. $N$ là trọng tâm $\triangle{MAB}$ (bạn tự CM $M, N, H$ thẳng hàng nhé)
Trước hết bạn CM $\triangle{GEK} \sim \triangle{JAO}$ (theo TH c-g-c, $\dfrac{GE}{JA} = \dfrac{KE}{OA} = \dfrac12$), từ đó CM $GK \parallel JO$. Ta sẽ đi CM $JO \perp BE$ hay $JO \perp BN$
Thật vậy. Ta có $\dfrac{GE}{JA} = \dfrac{IE}{BA} = \dfrac12$. Mà $\dfrac{GE}{IE} = \dfrac{2}3$ nên $\dfrac{JA}{BA} = \dfrac{2}3$. Suy ra $\dfrac{HJ}{HB} = \dfrac13$ (qua một số biến đổi), dẫn đến $\dfrac{HJ}{HB} = \dfrac{HN}{HM} (= \dfrac13)$
Theo định lý Ta-lét đảo thì $NJ \parallel MB$ hay $NJ \perp OB$. Có được $J$ là trực tâm $\triangle{ONB}$, ta suy ra $OJ \perp BN$. Ta có đpcm

 

[Thoòng Quốc An]

c) Dễ dàng CM được $\triangle{IBC} \sim \triangle{IAB}$ (g-g), suy ra $\dfrac{IB}{IA} = \dfrac{IC}{IB}$ hay $IB^2 = IA \cdot IC$
Ta sẽ CM $IM^2 = IA \cdot IC$. Thật vậy : $\widehat{IMC} = \widehat{ADC}$ (so le trong) và $\widehat{ADC} = \widehat{IAM}$ (góc nt = góc tạo bởi tia tiếp tuyến và dây cung cùng chắn một dây), suy ra $\widehat{IMC} = \widehat{IAM}$. Từ đây CM được $\triangle{IMC} \sim \triangle{IAM}$ (g-g), suy ra $\dfrac{IM}{IA} = \dfrac{IC}{IM}$ hay $IM^2 = IA \cdot IC$
Khi đó $IB^2 = IM^2$ hay $IB = IM$, ta thu được đpcm
d) Mình không biết là liệu có cách khác không, nhưng bạn thử tham thảo cách này. Mình chỉ vạch ra hướng đi thôi nhé
Gọi $J$ là giao điểm của tia $MG$ và $AB$, $H$ là giao điểm của $MO$ và $AB$. $N$ là trọng tâm $\triangle{MAB}$ (bạn tự CM $M, N, H$ thẳng hàng nhé)
Trước hết bạn CM $\triangle{GEK} \sim \triangle{JAO}$ (theo TH c-g-c, $\dfrac{GE}{JA} = \dfrac{KE}{OA} = \dfrac12$), từ đó CM $GK \parallel JO$. Ta sẽ đi CM $JO \perp BE$ hay $JO \perp BN$
Thật vậy. Ta có $\dfrac{GE}{JA} = \dfrac{IE}{BA} = \dfrac12$. Mà $\dfrac{GE}{IE} = \dfrac{2}3$ nên $\dfrac{JA}{BA} = \dfrac{2}3$. Suy ra $\dfrac{HJ}{HB} = \dfrac13$ (qua một số biến đổi), dẫn đến $\dfrac{HJ}{HB} = \dfrac{HN}{HM} (= \dfrac13)$
Theo định lý Ta-lét đảo thì $NJ \parallel MB$ hay $NJ \perp OB$. Có được $J$ là trực tâm $\triangle{ONB}$, ta suy ra $OJ \perp BN$. Ta có đpcm

Bạn vẽ hình minh họa giúp mình ko, mình đang giải lại nè!!! Cảm ơn!!! Chúc mừng thi hsg hạng nhất!!!

 

[iceghost]

Cám ơn bạn nhé, hì Hình minh họa đây bạn

 

[Thoòng Quốc An]

Cám ơn bạn nhé, hì Hình minh họa đây bạn
View attachment 6364

tui thi vật lý có giải ba thui!!!
Mấy câu này nữa nha câu d thôi!!!
14,15,16 câu d nha
cần gấp

 

[Thoòng Quốc An]

c) Dễ dàng CM được $\triangle{IBC} \sim \triangle{IAB}$ (g-g), suy ra $\dfrac{IB}{IA} = \dfrac{IC}{IB}$ hay $IB^2 = IA \cdot IC$
Ta sẽ CM $IM^2 = IA \cdot IC$. Thật vậy : $\widehat{IMC} = \widehat{ADC}$ (so le trong) và $\widehat{ADC} = \widehat{IAM}$ (góc nt = góc tạo bởi tia tiếp tuyến và dây cung cùng chắn một dây), suy ra $\widehat{IMC} = \widehat{IAM}$. Từ đây CM được $\triangle{IMC} \sim \triangle{IAM}$ (g-g), suy ra $\dfrac{IM}{IA} = \dfrac{IC}{IM}$ hay $IM^2 = IA \cdot IC$
Khi đó $IB^2 = IM^2$ hay $IB = IM$, ta thu được đpcm
d) Mình không biết là liệu có cách khác không, nhưng bạn thử tham thảo cách này. Mình chỉ vạch ra hướng đi thôi nhé
Gọi $J$ là giao điểm của tia $MG$ và $AB$, $H$ là giao điểm của $MO$ và $AB$. $N$ là trọng tâm $\triangle{MAB}$ (bạn tự CM $M, N, H$ thẳng hàng nhé)
Trước hết bạn CM $\triangle{GEK} \sim \triangle{JAO}$ (theo TH c-g-c, $\dfrac{GE}{JA} = \dfrac{KE}{OA} = \dfrac12$), từ đó CM $GK \parallel JO$. Ta sẽ đi CM $JO \perp BE$ hay $JO \perp BN$
Thật vậy. Ta có $\dfrac{GE}{JA} = \dfrac{IE}{BA} = \dfrac12$. Mà $\dfrac{GE}{IE} = \dfrac{2}3$ nên $\dfrac{JA}{BA} = \dfrac{2}3$. Suy ra $\dfrac{HJ}{HB} = \dfrac13$ (qua một số biến đổi), dẫn đến $\dfrac{HJ}{HB} = \dfrac{HN}{HM} (= \dfrac13)$
Theo định lý Ta-lét đảo thì $NJ \parallel MB$ hay $NJ \perp OB$. Có được $J$ là trực tâm $\triangle{ONB}$, ta suy ra $OJ \perp BN$. Ta có đpcm

làm sao để ra GE/JA= KE/OA = 1/2 mình phân vân chỗ đó và có căp góc nào băng để ra đồng dạng, mấy cái còn lại hiểu rồi

 

[iceghost]

làm sao để ra GE/JA= KE/OA = 1/2 mình phân vân chỗ đó và có căp góc nào băng để ra đồng dạng, mấy cái còn lại hiểu rồi

Bạn sử dụng tính chất đường trung bình, sử dụng cặp góc xen giữa các cặp cạnh tương ứng đó nhé bạn