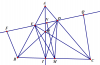
Cho tam giác ABC nhọn, đường cao BD, CE cắt nhau tại H. Gọi M là trung điểm của BC.
a)CM: tam giác EMD cân
b)Gọi F, Q là hình chiếu của B, C. CM: FE=DQ
c)CM: S tứ giác BEDC= S tam giác ABC . Sin²A
d)Kẻ đường cao AI.CM: H cách đều 3 cạnh tam giác EDI
e)Tìm Max: Sin A/2. Sin B/2. Sin C/2
Cảm ơn
_______________________
Phải gộp 2 cái đề này (Đề 1; Đề 2) lại mới thấy vừa ý, vừa đủ cho cái đề này!
________________________________________________
a) Ta có: [tex]EM=DM(=\frac{1}{2}BC)\Rightarrow \Delta EMD[/tex] cân
b) Kẻ đường cao $MN$. Suy ra $MN$ cũng là đường trung tuyến
[tex]\Rightarrow NE=ND[/tex]
Ta có: [tex]MN \parallel BE\parallel CQ[/tex]. Mà: $MB=MC$
[tex]\Rightarrow NF=NQ\Rightarrow NF-NE=NQ-ND\Rightarrow EF=DQ[/tex]
c) Bạn xem
Tại Đây!
d) Ta có: [tex]\widehat{AED}=\widehat{BEI}(=\widehat{ACB})[/tex]
Mà: [tex]\widehat{DEH}+\widehat{AED}=90^{\circ};\widehat{IEH}+\widehat{IEB}=90^{\circ}\Rightarrow \widehat{DEH}=\widehat{IEH}[/tex]
[tex]\Rightarrow EH[/tex] là phân giác [tex]\widehat{DEI}[/tex]
CMTT: [tex]DH[/tex] là phân giác góc [tex]\widehat{EDI}[/tex]
[tex]\Rightarrow H[/tex] là tâm đường tròn nội tiếp tam giác [tex]\Delta EDI\Rightarrow H[/tex] cách đều 3 cạnh của tam giác
e) Ta có:
K=[tex]sin\frac{A}{2}.sin\frac{B}{2}.sin\frac{C}{2}=\frac{1}{2}[cos(\frac{A-B}{2})-cos(\frac{A+B}{2})].sin\frac{C}{2}=\frac{1}{2}[cos(\frac{A-B}{2})-sin(\frac{C}{2})].sin\frac{C}{2}=\frac{1}{2}.cos.\frac{A-B}{2}.sin\frac{C}{2}-\frac{1}{2}.sin^2\frac{C}{2}-\frac{1}{8}.cos^2.\frac{A-B}{2}-\frac{1}{8}+\frac{1}{8}.cos^2.\frac{A-B}{2}+\frac{1}{8}[/tex]
K=[tex]\frac{-1}{2}(sin^2\frac{C}{2}-cos\frac{A-B}{2}.sin\frac{C}{2}+\frac{1}{4}cos^2.\frac{A-B}{2})-\frac{1}{8}(1-cos^2.\frac{A-B}{2})+\frac{1}{8}=\frac{-1}{2}(sin\frac{C}{2}-\frac{1}{2}cos.\frac{A-B}{2})^2-\frac{1}{8}(sin^2\frac{A-B}{2})+\frac{1}{8}\leq \frac{1}{8}[/tex]
Vậy $......$
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
