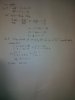Trắc nghiệm:
8, [tex]\underset{MN}{\rightarrow} = \left ( 1-m; 4 \right ) ; \underset{NP}{\rightarrow} = \left ( -3; -2 \right ).[/tex]
ĐỂ M; N; P thẳng hàng thì [tex]\frac{X(MN)}{X\left ( NP \right )} =\frac{Y\left ( MN \right )}{Y\left ( NP \right )}[/tex]
=> Thay số r tính ra m=-4.

9,Lần lượt thay hoành độ và tung độ của các véc tơ a,b,c vào hệ thức, ta đc hpt:
[tex]\left\{\begin{matrix} 3=2h -3k\\ -5= -2h +k \end{matrix}\right.[/tex]
<=> [tex]\left\{\begin{matrix} h=3\\ k=1 \end{matrix}\right.[/tex]
Tự luận:
2,c,
Đề bài cho là AM=4MB, đây là xét về độ dài, cách làm của bn là xét về vecto nên chưa chính xác.
Hướng làm của bài này là bn cx gọi tọa độ điểm M, rồi tính [tex]\underset{AM}{\rightarrow} ;\underset{MB}{\rightarrow}[/tex]
rồi tính độ dài theo công thức: [tex]\left | \underset{a}{\rightarrow} \right | = \sqrt{Xa^{2} +Ya^{2}}[/tex]
=> Ta có pt về độ dài và 1pt về A;B;M thẳng hàng . giải bpt => x,y


 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.