Toán Hình về tính số đo góc

[hbo_bobaby]

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

Cho tam giác ABC có góc A=60 độ. Kẻ 2 đường phân giác CE và BF của tam giác ABC chúng cắt nhau tại I. Chứng minh góc IEF= góc IFE.

Câu hỏi event

 

[vy000]

Ta có:

$\widehat{FIE}=\widehat{IFB}+\widehat{IBF}= \widehat{BAC}+\widehat{ACF}+\widehat{ABE}=\widehat{BAC}+\dfrac12(\widehat{ABC}+\widehat{ACB})= \widehat{BAC}+\dfrac12(180^o-\widehat{BAC})=120^o$

$\Rightarrow AEFI \text{nội tiếp}$

$\Rightarrow \widehat{EFI}=\widehat{IAE}=\widehat{IAF}=\widehat{IEF}$

Chứng tỏ....
@Tú: Chú ý giải bằng kiến thức lớp 8

 

[toiyeutee]

Loi giai ne

Ta co:goc a =60' suy ra tam giac abc la tam giac deu suy ra goc b ;goc c deu=60' ma ta lai co tong 4 goc cua 1 tu giac la 360'

 

[harrypham]

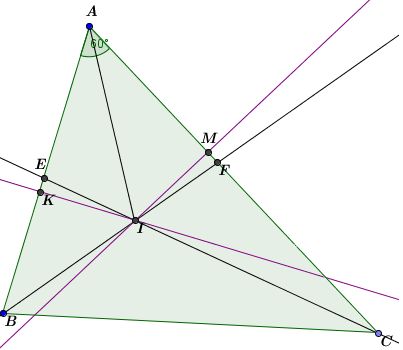
Kẻ [TEX]IK \perp AB, \; IM \perp AC[/TEX].
Do hai tia phân giác của góc [TEX]B,C[/TEX] cắt nhau tại [TEX]I[/TEX] nên [TEX]AI[/TEX] là phân giác góc [TEX]A[/TEX].
Khi đó [TEX]\widehat{BAI}= \widehat{IAC}=30^o[/TEX].
Dễ dàng chứng minh được [TEX]\triangle AIK = \triangle AIM[/TEX] (cạnh huyền, góc nhọn)
Suy ra [TEX]IK=IM[/TEX] và [TEX]\widehat{AIK}= \widehat{AIM}=60^o \Rightarrow \widehat{KIM}=120^o[/TEX]. (1)

Lại có do [TEX]\widehat{A}=60^o \Rightarrow \widehat{B}+ \widehat{C}=120^o \Rightarrow \widehat{IBC}+ \widehat{ICB}=60^o \Rightarrow \widehat{BIC}=120^o[/TEX].
Hay [TEX]\widehat{KIF}=120^o[/TEX]. (2)

Từ (1) và (2) thì [TEX]\widehat{KIM}= \widehat{KIF}=120^o \Rightarrow \widehat{EIK}= \widehat{MIF}[/TEX].

Như vậy xét tam giác vuông [TEX]KIE[/TEX] và [TEX]MIF[/TEX] có
+ [TEX]IK=IM[/TEX].
+ [TEX]\widehat{EIK}= \widehat{MIF}[/TEX]
[TEX]\Rightarrow \triangle KIE = \triangle MIF[/TEX]
[TEX]\Rightarrow IE=IF[/TEX] nên tam giác [TEX]IFE[/TEX] cân ở [TEX]I[/TEX].
Suy ra [TEX]\widehat{IEF} = \widehat{IFE}[/TEX].
Ta có đpcm.