Toán hình học 7

P

ptthao_2002

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

[FONT=&quot]Bài 1:[/FONT][FONT=&quot] [/FONT][FONT=&quot]Cho tam giác ABC cân ở A; vẽ BD và CE thứ tự vuông góc với AC và AB
a) C/m BD = CE
b) Gọi H là giao điểm của BD;CE. C/m HD = HE (chủ yếu là giúp e câu b với ạh)

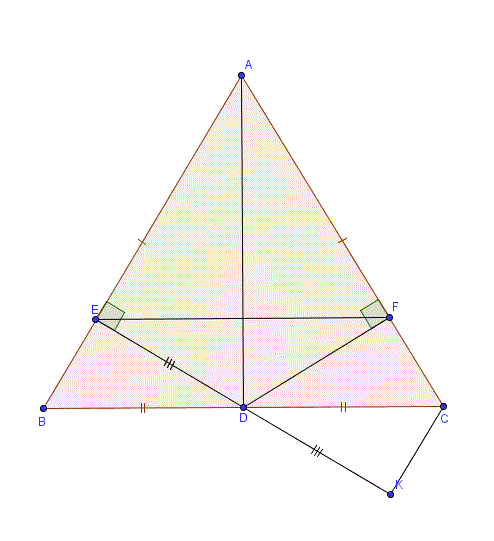
Bài 2: Cho tam giác ABC ( AB = AC). Gọi D là trung điểm của BC. Từ D hạ DE;DF thứ tự vuông góc với AB;AC.
a) C/m [tex]\large\Delta[/tex]ADE = [tex]\large\Delta[/tex]AFD và AD là đường trung trực của đoạn thẳng EF.
b) Trên tia đối của tia DE lấy điểm K sao cho DE = DK
C/m [tex]\large\Delta[/tex] DKC vuông.

Bài 3: Cho [tex]\large\Delta[/tex] cân ABC có AB = AC = 5 cm, BC = 8 cm, kẻ AH vuông góc với BC ( H thuộc BC)
a) C/m: HB = HC và [TEX]\hat{BAH}[/TEX] = [TEX]\hat{CAH}[/TEX]
b) Tính độ dài AH
c) Kẻ HD;HE thứ tự vuông góc với AB;AC ( D [tex]\epsilon[/tex] AB; E [tex]\epsilon[/tex] AC). C/m [tex]\large\Delta[/tex] HDE cân

Bài 4: Cho [tex]\large\Delta[/tex] ABC vuông A. AC =12cm,BC =13cm, I là trung điểm của BC, trên tia AI lấy điểm D sao cho AI bằng ID.
a) Tính AB.
b) C/m [tex]\large\Delta[/tex]IDC = [tex]\large\Delta[/tex] IAB. Suy ra [tex]\large\Delta[/tex] ADC vuông.
c) Cho M là trung điểm của AC. C/m MB=MD.
d) Gọi E và N lần lượt là giao điểm của MD với CB,MB với AD. C/m MEN cân.

Bài 5:
Cho tam giác ABC cân tại A. Kẻ AH vuông góc với BC, lấy điểm D sao cho C là trung điểm của BD. Trên tia đối của tia HA lấy điểm I sao cho HI = HA. Chứng minh :
a/ HB = HC và AB = IC[/FONT]
[FONT=&quot]b/ [tex]\large\Delta[/tex] ADI cân và C là trọng tâm của [tex]\large\Delta[/tex] ADI.[/FONT]
[FONT=&quot]c/ Gọi M là trung điểm của AD. Chứng minh CM // AB.[/FONT]
[FONT=&quot] m.n giúp e nha, e cần gấp trong tuần này @};-:)
[/FONT]
 
S

sonsuboy

câu 1:tam giác AEC=tam giác ADB(cgc)
-->AE=AD(1)
Do tam giác ABC cân tại A-->AB=AC(2)
Từ 1 và 2-->BE=DC
tam giác EHB=tam giác DHC(gcg)
-->HE=HD
 
S

sonsuboy

góc HEB=góc HDC=90o(1)
góc EHB=góc DNC(đối đỉnh)
Từ 1 và 2-->
góc HBE=góc HCD
 
T

thaotran19

Bài 3 :
a)Vì $\triangle ABC $ cân tại A nên AH là đg cao đồng thời cx là đg p/g, đường trung tuyến.
\Rightarrow $HB = HC$ và $\hat{BAH} = \hat{CAH}$
b)$HC=\dfrac{BC}{2}=\dfrac{8}{2}=4$
Áp dụng định lý Py-ta-go vào tam gíác vuông AHC có:
$AH^2=AC^2-HC^2=.......$
\Rightarrow $AH=...........$
c)Xét 2 tam gíác vuông : BDH và CEH có
HB=HC(cmt)
$\hat{B}=\hat{C}(\triangle ABC~ cân)$
Do đó: $\triangle BDH =\triangle CEH $
\Rightarrow DH =EH
\Rightarrow dpcm
 
P

phamhuy20011801

Bài 5:
a, Do tam giác ABC cân tại A nên đường cao AH cũng là trung tuyến \Rightarrow BH=HC.
BH=HC; góc AHB=góc CHI; AH=HI
Suy ra tam giác ABH bằng tam giác ICH (c.g.c)
Suy ra AC=IC.
b, Ta có: $CH=\frac{BC}{2}=\frac{CD}{2}=\frac{BD}{4}=\frac{HD}{3}(BH=HC)$
AH=HI
Ta có: $CH=\frac{1}{3}.HD$ và AH=HI nên...(đpcm)
c,
Tam giác ABH bằng tam giác ICH (cmt)
Suy ra góc BAH bằng góc CIH
Suy ra IC // AB
Suy ra CM//AB (do I,C,M thẳng hàng).
 
I

iceghost

ptthao_2002 said:
Bài 2: Cho tam giác ABC ( AB = AC). Gọi D là trung điểm của BC. Từ D hạ DE;DF thứ tự vuông góc với AB;AC.
a) C/m [tex]\large\Delta[/tex]ADE = [tex]\large\Delta[/tex]AFD và AD là đường trung trực của đoạn thẳng EF.
b) Trên tia đối của tia DE lấy điểm K sao cho DE = DK
C/m [tex]\large\Delta[/tex] DKC vuông.
Bấm để xem đầy đủ nội dung ...
20_zpsvfkmvwjc.gif


a)Ta có : AB = AC
\Rightarrow $\triangle$ ABC cân tại A

Xét $\triangle$ ABC cân tại A có :
AD là đường trung tuyến
\Rightarrow AD là đường phân giác

Xét $\triangle$ ADE vuông tại E và $\triangle$ ADF vuông tại F có :
AD là cạnh chung
$\widehat{DAE} = \widehat{DAF}$ ( AD là đường phân giác )
Vậy $\triangle$ ADE = $\triangle$ ADF (ch-gn)

\Rightarrow AE = AF ( hai cạnh tương ứng )
\Rightarrow A nằm trên đường trung trực của EF (1)
Lại có : DE = DF ( $\triangle$ ADE = $\triangle$ ADF )
\Rightarrow D nằm trên đường trung trực của EF (2)
Từ (1), (2) \Rightarrow AD là đường trung trực của EF

b)Xét $\triangle$ DEB và $\triangle$ DKC có :
DE = DK ( gt)
$\widehat{EDB} = \widehat{KDC}$ ( đối đỉnh )
BD = CD ( D là trung điểm BC )
Vậy $\triangle$ DEB = $\triangle$ DKC (c.g.c)
\Rightarrow $\widehat{DEB} = \widehat{DKC} $ ( hai góc tương ứng )
Mà $\widehat{DEB} = 90^o$
\Rightarrow $\widehat{DKC} = 90^o$
\Rightarrow $\triangle$ DKC vuông tại K :)
 
P

ptthao_2002

phamhuy20011801 said:
Bài 5:
a, Do tam giác ABC cân tại A nên đường cao AH cũng là trung tuyến \Rightarrow BH=HC.
BH=HC; góc AHB=góc CHI; AH=HI
Suy ra tam giác ABH bằng tam giác ICH (c.g.c)
Suy ra AC=IC.
b, Ta có: $CH=\frac{BC}{2}=\frac{CD}{2}=\frac{BD}{4}=\frac{HD}{3}(BH=HC)$
AH=HI
Ta có: $CH=\frac{1}{3}.HD$ và AH=HI nên...(đpcm)
c,
Tam giác ABH bằng tam giác ICH (cmt)
Suy ra góc BAH bằng góc CIH
Suy ra IC // AB
Suy ra CM//AB (do I,C,M thẳng hàng).
Bấm để xem đầy đủ nội dung ...

Phải chứng minh I,C, M thẳng hàng nữa ạh :)
Mà chứng minh thế nào v ạh :cool::)>-
 
P

phamhuy20011801

@ptthao_2002
5a, Cần nói thêm AB=AC đã
c, I,C,M thẳng hàng do C là trọng tâm tam giác ADI (câu b), IM là trung tuyến xuất phát từ I của tam giác ADI nên luôn đi qua trọng tâm.
IM đi qua C thì I,C,M thẳng hàng.
 
V

vandamphongkhinh

Bài 4: Cho [tex]\large\Delta[/tex] ABC vuông A. AC =12cm,BC =13cm, I là trung điểm của BC, trên tia AI lấy điểm D sao cho AI bằng ID.
a) Tính AB.
b) C/m [tex]\large\Delta[/tex]IDC = [tex]\large\Delta[/tex] IAB. Suy ra [tex]\large\Delta[/tex] ADC vuông.
c) Cho M là trung điểm của AC. C/m MB=MD.
d) Gọi E và N lần lượt là giao điểm của MD với CB,MB với AD. C/m MEN cân.

--------------

2 câu a và b dễ nên mình sẽ không làm bạn tự làm nhé.
từ câu b có thể => ABDC là hcn => BAM = MCD = 90 ; AI = ID = BI = IC ; AB = CD ; AD = BC

c) chứng minh tam giác BAM = DCM ( cạnh góc cạnh )
=> MB = MD
d) - Chứng minh tam giác BMC = DMA ( cạnh cạnh cạnh )
=> MBC = MDA
- chứng minh tam giác INB = IEC
CÓ MBC= MDA
BI = ID
NIB = EID ( đối đỉnh )
=> NI = IE
=> tam giác INE cân I
=> INE = IEN
- theo góc ngoài trong tam giác
NEM = MDN + INE
ENM = MBE + IEN
mà các góc bằng nhau theo cm trên
=> NEM = ENM
=> TAM GIÁC CÂN
;);)
 
Last edited by a moderator:
You must log in or register to reply here.
Top Bottom