[TOÁN HÌNH] đề thi toán học kì II

[lovely_girl2002]

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

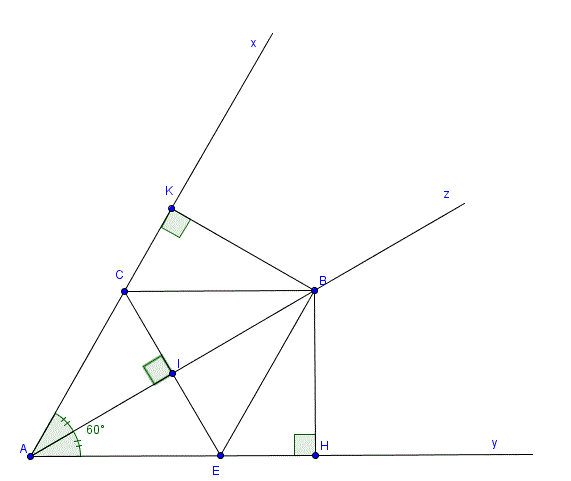
Cho [TEX]\widehat{x A y}[/TEX] = [TEX]60^o[/TEX] có tia phân giác Az. Từ một điểm B trên tia Ax kẻ BH [TEX]\bot[/TEX] Ay, BK [TEX]\bot[/TEX] Az và kẻ Bt // Ay, Bt cắt Az tại C.
a) Chứng minh [TEX]\Delta [/TEX]ABC là tam giác cân
b) Chứng minh [TEX]\Delta [/TEX]ABH = [TEX]\Delta [/TEX]BAK
c) Từ C kẻ CE [TEX]\bot[/TEX] Ay. Chứng minh [TEX]\Delta [/TEX]CEK là tam giác đều.


Giúp mình nha. Cảm ơn!!!

 

[iceghost]

a)Ta có : $\widehat{BAC} = \widehat{zAy}$ ( Az là tia phân giác $\widehat{xAy}$ )
Mà $\widehat{zAy} = \widehat{ABC}$ ( so le trong, $BC // Ay$ )
\Rightarrow $\widehat{BAC} = \widehat{ABC}$
\Rightarrow $\triangle$ ABC cân

b)Xét $\triangle$ ABH vuông tại H và $\triangle$ ABK vuông tại K có :
AB là cạnh chung
$\widehat{BAH} = \widehat{BAK}$ ( Az là tia phân giác $\widehat{xAy}$ )
Vậy $\triangle$ ABH = $\triangle$ ABK ( ch-gn )

c)Sai đề, đã sửa (nhưng không biết đúng không )
Xét $\triangle$ ACI vuông tại I và $\triangle$ AEI vuông tại I có :
AI là cạnh chung
$\widehat{CAI} = \widehat{EAI}$ ( Az là tia phân giác $\widehat{xAy}$)
Vậy $\triangle$ ACI = $\triangle$ AEI ( g.c.g )
\Rightarrow CI = EI ( hai cạnh tương ứng )

Xét $\triangle$ BCE có :
BI là đường cao đồng thời là đường trung trực
\Rightarrow $\triangle$ BCE cân (1)

Ta có : BC = AC ( $\triangle$ ABC cân )
Mà BC = BE ( $\triangle$ BCE cân )
\Rightarrow AC = BE

Xét $\triangle$ BEI vuông tại I và $\triangle$ ACI vuông tại I có :
BE = AC (cmt)
EI = CI ( cmt)
Vậy $\triangle$ BEI = $\triangle$ ACI (ch-cgv)
\Rightarrow $\widehat{EBI} = \widehat{CAI}$ ( hai góc tương ứng )

Ta có : $\widehat{CAI} + \widehat{EAI} = 60^o$
$\widehat{CBI} + \widehat{EBI} = \widehat{CBE}$
Mà $\widehat{CAI} = \widehat{EBI}$ ( cmt )
$\widehat{EAI} = \widehat{CBI}$ ( so le trong, BC // Ay )
\Rightarrow $\widehat{CBE} = 60^o$(2)
Từ (1), (2) \Rightarrow $\triangle$ CEB đều