toán hình cực khó

[linhkosoai]

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

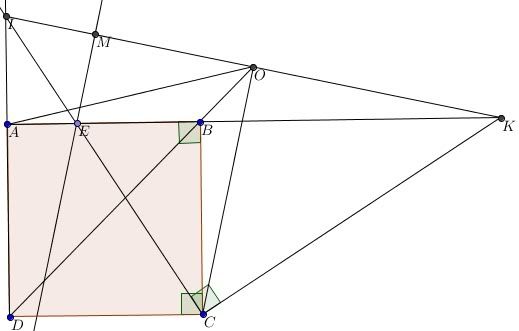
Cho hình vuông ABCD cạnh a,E là điểm bất kì nằm giữa A va B, đường thẳng CE cắt đường thẳng AD tại I, đường thẳng vuông góc với CI tại C cắt đường thẳng AB tại K.
a/ Chứng minh rằng tứ giác ACKI nội tiếp và CI =CK. suy ra trung điểm của IK di động trên 1 đường cố định.
b/ Từ E kẻ đường vuông góc với IK tại M, khi E di động trên AB, chứng tỏ M di động trên đường cố định.
c/ Đặt BE=x,tinh các độ dài BK,CK,IK và diện tích tứ giác ACKI theo a va x.
toán thi học sinh giỏi cấp quốc gia jup mình với

 

[harrypham]

a) Câu này mình không hiểu lắm tứ giác nội tiếp là gì nên ...
Ta có $\triangle KBC= \triangle IDC$ (g.c.g) vì $BC=DC, \; \widehat{IDC}= \widehat{KBC}=90^o, \; \widehat{KCB}= \widehat{ICD}$ (cùng phụ với $\widehat{ECB}$).
$\implies IC=CK$.

Gọi $O$ trung điểm $IK$. Nối $AO,OC$.
Ta có $AO$ là trung tuyến ứng với cạnh huyền $IK$ của tam giác vuông $IAK$ nên $AO= \dfrac{1}{2}IK$. Tương tự $OC$ là trung tuyến ứng với cạnh huyền của tam giác vuông $ICK$ nên $CO= \dfrac{1}{2}IK$.
Do đó $AO=OC \implies \triangle ODA= \triangle ODC \; (\text{c.c.c}) \implies \widehat{ODA}= \widehat{ODC}=45^o \text{ } (1)$

Ta cũng có $\triangle BDA= \triangle BDC \implies \widehat{BDA}= \widehat{BDC}=45^o \text{ } (2)$.

Từ $(1)$ và $(2)$ suy ra ba điểm $O,B,D$ thẳng hàng.
Cho nên điểm $O$ thuộc đường phân giác góc $ADC$ (đường cố định).


​