Toán hay đây!!!!!!!!!

M

muttay04

hók búa wá!!!!!!!

depvazoi said:
Cho tam giác ABC cân tại A có góc A<90 độ. Kẻ BH vuông góc AC (H thuộc AC). Gọi D là điểm tuỳ ý trên cạnh BC. Kẻ DE vuông góc AB (E thuộc AB), DF vuông góc AC (F thuộc AC). Chứng minh: DE+DF=BH.
Bấm để xem đầy đủ nội dung ...
Bài này khó wá bạn ạ!!! Mình hok bít có đúng hok nữa;););););););)
untitl11.jpg

kéo dài đoạn thẳng chứa D cắt AB tại G
-----------===>tam giác GBD cân tại G
Do BHF^=HFD^=90*=>DF=IH(cái này mìn làm chưa chắc lắm)
==>DF song song với BH
\Rightarrow\Rightarrow DIH^=90*
======================>Xét tam giác EDB và IDB
\Rightarrow BI=ED
=>đpcm
THANKS MÌN NHÉ
 
C

chipxinh148

Trên tia đối của tia DF ta vẽ DE’ sao cho DE’ = DE
Ta có: EDB + EBD = 90 độ
FDC + FCD = 90 độ
Mà FCD = EBD =>góc EDB = góc FDC (1)
Do BDE’ và FDC là 2 góc đối đỉnh nên BDE’ = FDC (2)
Từ và => FDB = BDE’
*Xét t.giác EBD và t.giác E’BD,ta có:
ED = E’D
FDB = BDE’
BD là cạnh chung => t.giác EBD = t.giác E’BD (cgc)
 Góc EBD = góc DBE’
Mà EBD = ACB => góc DBE’ = góc ACB
Ta có : DBE’ = ACB ; DBE’ và ACB ở cùng vị trí sole trong => AC // BE
Ta có: AC // BE ; FHB và E’BH ở cùng vị trí trong cùng phía => E’BH = FHB = 90 độ
Ta có: E’BF + FBH = 90 độ
HFB + BFE’ = 90 độ
Mà E’BF = HFB (AC // BE và ở cùng vị trí sole trong) => FBH = BFE’
*Xét HBF và E’FB , ta có:
BF là cạnh chung
FBH = BFE’ (cmt)
E’BF = HFB (cmt) => t.giác HBF = t.giác E’FB
=> BH = FE’
Ta có: BH =FE’=FD + DE’ = FD + DE (đpcm)
 
H

harrypham

Bài này có 3 cách, xin giới thiệu với các bạn. (trước khi đọc khuyên mọi người nên đọc cách 3 trước, cách này rất đặc sắc)

Cách 1.
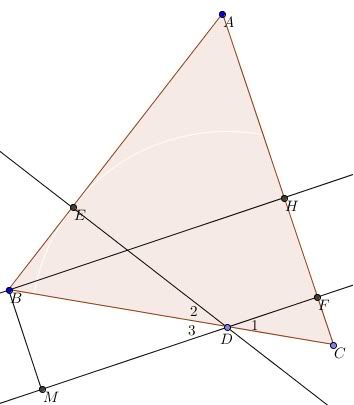
untitled-39.jpg

Trên tia đối tia DF lấy M sao cho [TEX]DM=DE[/TEX].
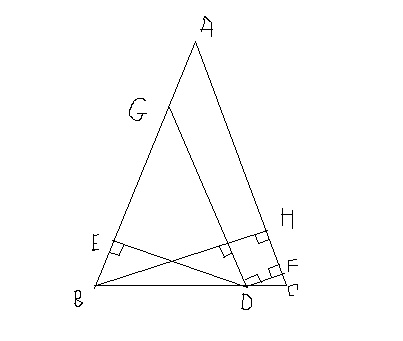
Xét hai tam giác DEB và DFC có [TEX]\widehat{E}= \hat{F} =90^o, \; \hat{B}= \hat{C}[/TEX] (gt) nên [TEX]\hat{D_1}= \hat{D_2}[/TEX] mà [TEX]\hat{D_2}= \hat{D_3}[/TEX] (đđ) nên [TEX]\hat{D_1} = \hat{D_3}[/TEX].

Khi đó [TEX]\triangle DBE = \triangle DBM[/TEX] (c.g.c) nên [TEX]\hat{E} = \hat{M} = 90^o[/TEX].

Do vậy [TEX]HB // FN \ ( \perp BM); \; BM //HF \ (\perp MF)[/TEX], nên [TEX]BH=MF[/TEX] hay [TEX]BH=MD+DF = DE+DF[/TEX].

Cách 2.
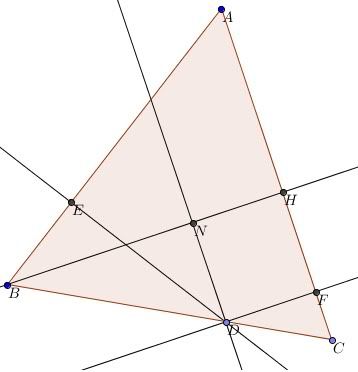
untitled-40.jpg

Kẻ [TEX]DN \perp BH[/TEX]. Ta có [TEX]DN // HF \ (\perp BH); \; NH//DF \ (\perp HF)[/TEX] nên [TEX]NH=DF[/TEX]. Bây giờ cần chứng minh [TEX]BN=ED[/TEX].

Xét tam giác EDB và NBD có
+ Chung BD
+ [TEX]\hat{E}= \hat{N} \ (=90^o)[/TEX]
+ [TEX]\widehat{NDB}= \widehat{ACB}[/TEX] (do [TEX]DN//HF[/TEX])
mà [TEX]\widehat{ACB}= \widehat{ABC}[/TEX] nên [TEX]\widehat{ABC}= \widehat{NDB}[/TEX].
[TEX]\Rightarrow \triangle EDB= \triangle NBD[/TEX] (cạnh huyền - góc nhọn)
[TEX]\Rightarrow ED=BN[/TEX].

Vậy [TEX]BH=BN+NH=ED+DF[/TEX] (đpcm)

Cách 3.
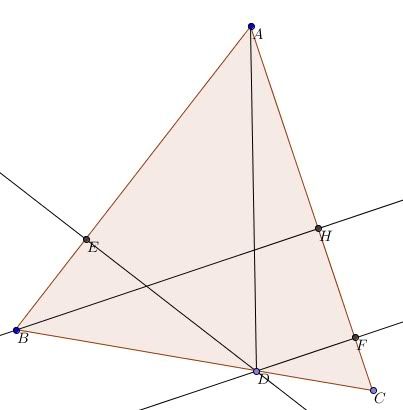
untitled-41.jpg

Nối A với D. Ta có
[TEX]2.S_{ABC}= BH.AC[/TEX]
[TEX]2.S_{ABC}= 2.S_{ADB}+ 2.S_{ADC} = ED.AB+DF.AC=(ED+DF).AC[/TEX]​

Vậy [TEX]2.S_{ABC}=BH.AC=(ED+DF).AC[/TEX] nên [TEX]BH=ED+DF[/TEX].
 
You must log in or register to reply here.
Top Bottom