Toán toán câu 4

[Anhdepzailol 1020]

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

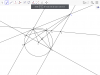
Câu 4. Cho đường tròn O và 1 điểm A sao cho OA=3R. Qua A kẻ hai tiếp tuyến AP và AQ của đường tròn (O), với P và Q là 2 tiếp điểm. Lấy M thuộc đường tròn (O) sao cho PM song song với AQ. Gọi N là giao điểm thứ hai của đường thẳng AM và đường tròn (O). Tia PN cắt đường thẳng AQ tại K.
1. CM Tg APOQ nội tiếp
2. CM KA^2=KN.KP
3. Kẻ đường kính QS của đường tròn (O). CM tia NS là phân giác của góc PNM
4. Gọi G là giao điểm của 2 đường thẳng AO và PK. Tính độ dài đoạn thẳng AG theo R ( câu này mik lm chỉ cần tính đc GH nx thôi là mik xog nhưng khó quá, còn bạn nào có cách tính AG khác thì giúp mik vs)
Mik đag cần gấp!!!!!!!!!Xin cảm ơn

 

[Nguyễn Xuân Hiếu]

Đầu tiên bạn cm: $\triangle QNK$ và $\triangle PQK$ (g.g)
$\Rightarrow QK^2=KN.KP$.
Mà ở câu 2 $KA^2=KN.KP$.
Do đó $AK=QK$.
Mặt khác gọi $H$ là giao điểm của $OA$ và $PQ$.
Dễ dàng chứng minh: $HP=HQ$.
Xét tam giác $APQ$ dễ thấy $G$ là trọng tâm.
Do đó $\dfrac{AG}{OA}=\dfrac{2}{3}$.
Tới đây dễ rồi :V