P
phantrang97
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
1.Giải các phương trình:
%20\sqrt{2-{x}^{2}}+%20\sqrt{2-\frac{1}{{x}^{2}}}=%204%20-%20(x+%20\frac{1}{x}))
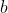%20\sqrt{x-2\sqrt{x-1}}%20+%20\sqrt{x+3-4\sqrt{x-1}}=1)
%20{x}^{2}+%20x%20+%2012\sqrt{x+1}=36)
2.a) Cho

Chứng minh rằng:

b) Cho a >= 0
Chứng minh rằng:

c) Cho a, b,c là 3 cạnh của một tam giác và 0 =< t =< 1
Chứng minh rằng:

3. a) Trong hình chữ nhật 3 x 4 đặt 6 điểm.Cm rằng trong các điểm này tìm được hai điểm mà khỏang cách giữa chúng không lớn hơn
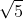
b) Cm rằng nếu n lẻ ( n thuộc N) thì
 không là số chính phương.
không là số chính phương.
WHO CAN DO IT?
2.a) Cho
Chứng minh rằng:
b) Cho a >= 0
Chứng minh rằng:
c) Cho a, b,c là 3 cạnh của một tam giác và 0 =< t =< 1
Chứng minh rằng:
3. a) Trong hình chữ nhật 3 x 4 đặt 6 điểm.Cm rằng trong các điểm này tìm được hai điểm mà khỏang cách giữa chúng không lớn hơn
b) Cm rằng nếu n lẻ ( n thuộc N) thì
WHO CAN DO IT?

