[Toán 9] CMR MM',NN',PP' đồng quy

[cutebest]

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

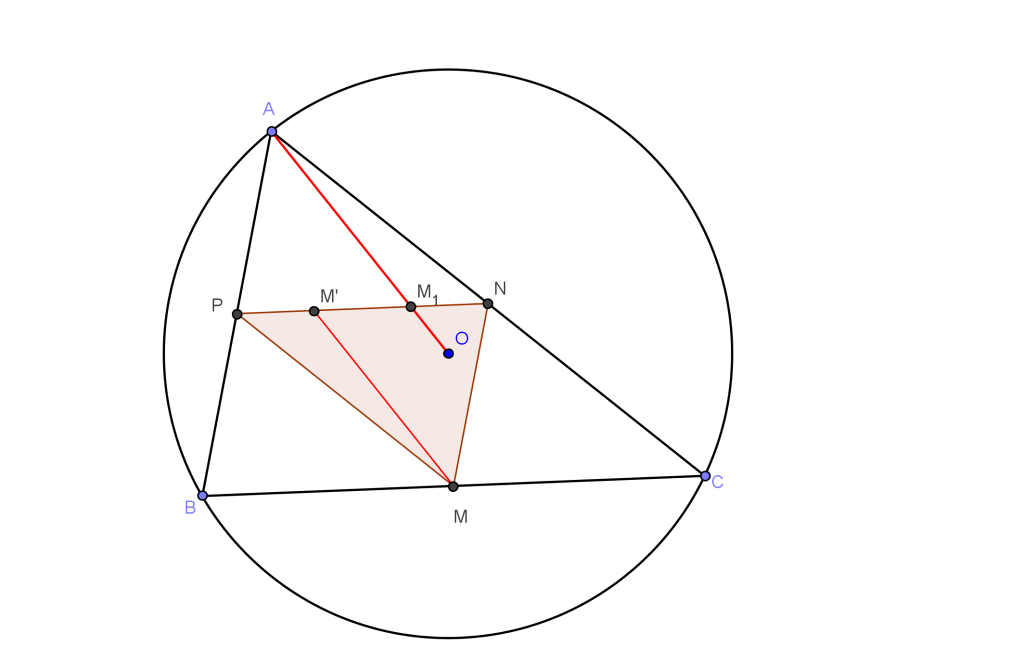
cho tam giác ABC nội tiếp đường tròn tâm (O,R),.Gọi M,N,P lần lượt là trung điểm của các cạnh BC,AC,AB.Vẽ các đường thẳng MM'//OA,NN'//OB,PP'//OC.
crm MM',NN',PP' đồng quy
các vị nào làm giúp thacks

 

[minhtuyb]

Hiện tại anh chưa tìm ra lời giải THCS cho bài này. Anh post tạm lời giải THPT (ứng dụng tâm tỉ cự) để giải quyết bài này. Có thể 1 năm sau đọc lại em sẽ hiểu :-"

-Giả sử $M'\in NP$. Gọi $M_1$ là giao điểm $OA$ với $NP$.
Ta có:
$$O=\dfrac{\sum \sin 2A.A}{\sum \sin 2A}=\dfrac{(\sin2A-\sin2B-\sin2C)A+2\sin2B.P+2\sin2C.N}{\sum \sin 2A}\ (1)$$
Xét phép chiếu $P_{j\ OA}^{\ \ NP}: O,A \mapsto M_1\ ;\ N\mapsto N\ ;\ P\mapsto P$. Chiếu hệ tâm tỉ cự $(1)$ xuống ta có:
$$M_1=\dfrac{(\sin2A-\sin2B-\sin2C)M_1+2\sin2B.P+2\sin2C.N}{\sum \sin 2A}\\ \Rightarrow M_1=\dfrac{\sin2B.P+\sin2C.N}{\sin2B+\sin2C}$$

-Mặt khác:
$$2M=B+C=C+A+B+A-2A=2N+2P-2A\\ \Rightarrow M=N+P-A\ (2)$$
Xét phép chiếu $P_{j\ OA}^{\ \ NP}: M \mapsto M'\ ;\ A\mapsto M_1\ ;\ N,P\mapsto N,P$. Chiếu hệ tâm tỉ cự $(2)$ xuống ta có:
$$M'=N+P-M_1=N+P-\dfrac{\sin2B.P+\sin2C.N}{\sin2B+\sin2C}=\dfrac{\sin2C.P+\sin2B.N}{\sin2B+\sin2C}\Rightarrow (M' ,NP)= -\dfrac{\sin2C}{\sin2B}$$

Chứng minh tương tự rồi cộng lại ta có:$(M' ,NP).(N' ,PM).(P' ,MN)=-1\Rightarrow MM',NN',PP'$ đồng quy (định lý $Ceva$, với chú ý các đường này đôi một không song song)

Bài toán được c/m $\square$