Toán [TOÁN 9] Bài tập hình học

[duy khiem tran]

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

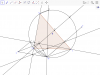
Cho tam giác ABC nhọn nooijt iếp đường tròn (O) . Hai đường cao BD và CE của tam giác ABC giao nhau tại H.
a) CM : BEDC nội tiếp và AH vuông BC
b) Vẽ dây MN vuông góc với BC tại K ( M thuộc cung nhỏ BC) . Đường thẳng đi qua K và song song với AN cắt MH ở I. . Gọi giao điểm của IK với AC , AB lần lượt là S và F. CM MS vuông AC và MF vuông AB
c) Gọi Q là điểm đối xứng với M qua AB và G là điểm đối xứng với M qua AC. CM 3 điểm Q,H,G thẳng hàng.
d) CM I là trung điểm MH
thanks mọi ng !!

 

[iceghost]

a) Bạn tự giải nhé
b) Có $\widehat{NKS} = \widehat{ANK} = \widehat{ACM}$ nên $MKSC$ nt, suy ra $\widehat{MSC} = \widehat{MKC} = 90^\circ$ hay $MS \perp AC$. Tương tự ta cũng có $MF \perp AB$
c) Có $\widehat{AQB} = \widehat{AMB} = \widehat{ACB} = 180 - \widehat{AHB}$ nên $AQBH$ nt, suy ra $\widehat{AHQ} = \widehat{ABQ} = \widehat{ABM}$. Tương tự ta cũng có $\widehat{AHG} = \widehat{ACM}$, suy ra $\widehat{AHQ} + \widehat{AHG} = 180^\circ$ hay $Q, H, G$ thẳng hàng
d) Có $\widehat{AHQ} = \widehat{ABQ} = \widehat{ABM} = 180^\circ - \widehat{ANM} = \widehat{NAH}$ nên $QG \parallel AN \parallel FS$
Mà $FS$ đi qua trung điểm $MQ$ nên cũng đi qua trung điểm của $MH$, hay $I$ là trung điểm của $MH$

 

[Nguyễn Xuân Hiếu]

Cách khác
câu c) Gọi giao điểm của $CH,BH$ với đường tròn (O) là $J,L$.
Dễ dàng chứng minh: $J$ đối xứng với $H$ qua $E$.
Do đó: $JHMQ$ là hình thang cân.
$\Rightarrow \widehat{HQM}=\widehat{HJM}=\widehat{CBM}=\widehat{KFM}$.
Do đó: $QH//FS$ tương tự cũng có $HG//FS$ do đó $Q,H,G$ thẳng hàng .