H
hoa_giot_tuyet
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Kết thúc vòng I rồi, những bạn chưa có điểm hay điểm hơi thấp thì cố lên nha ở vòng II nha. :Mfoyourinfo: Thang điểm vòng II là 100đ. Kết quả điểm vòng I xem tại đây http://diendan.hocmai.vn/showthread.php?t=138913
Vòng II
Câu 1. a) (5điểm) Cho dãy số [tex]1,3,6,10,15,..., \ \ \frac{n(n+1)}{2}[/tex]
Chứng tỏ rằng tổng của 2 số liên tiếp trong dãy luôn là số chính phương.
b) Một số tự nhiên có 5 chữ số. Nếu viết thêm 1 số vào bên trái hay bên phải số đó ta đều được một số có 6 chữ số. Biết rằng nếu viết thêm vào bên phải số đó thì được một số mới gấp 3 lần ta viết thêm vào bên trái. Hãy tìm số đó. (10điểm)
Câu 2 (15điểm). Phân tích đa thức thành nhân tử
a)[tex]x^4+6x^3+7x^2-6x+1[/tex]
b) [tex](x^2+y^2+z^2)(x+y+z)^2 + (xy+yz+xz)^2[/tex]
Câu 3.(15điểm) a) Cho [tex]a^3 - 3ab^2 = 19[/tex], [tex]b^3 - 3a^2b = 97[/tex]. Tính [tex]a^2+b^2[/tex]
b) Giải phương trình
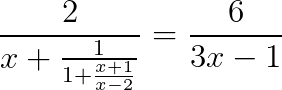
Câu 4.(20điểm) Cho tứ giác ABCD. Đường thẳng qua A và song song với BC cắt BD ở E. Đường thẳng qua B và song song với AD cắt AC ở F. Chứng minh EF//DC.
Câu 5(25điểm). Cho hình thang cân ABCD có AB//CD, AB<CD. Độ dài đường cao BH bằng đường trung bình của hình thang ABCD. Chứng minh BD vuông góc với AC
Câu 6(10). Tìm giá trị lớn nhất hoặc nhỏ nhất của biểu thức:
[tex]B = -x^2 + 2xy - 4y^2 + 2x + 10y - 8[/tex]
[tex] C = \frac{x}{(x+10)^2}[/tex]
Chú ý:
Thí sinh gửi bài làm theo 2 cách sau:
Cách 1: Gửi trực tiếp bài giải cho hoa_giot_tuyet tại đây. <~ click
Cách 2: Soạn bằng file Word và gửi về email : thiensu_snowdrop@yahoo.com
Hạn chót nộp bài là ngày 20/3/2011
Để tránh hiện tượng SPAM và POST nhầm bài giải vào đây TOPIC sẽ được khóa.
Thanks
Ai gửi bài cho mik` rồi thì tks một cái nhá ) nếu mà tiếc thanks thì sau này xoá cảm ơn cũng đc ^^ để tránh sự thất lạc bài gửi thôi :|
) nếu mà tiếc thanks thì sau này xoá cảm ơn cũng đc ^^ để tránh sự thất lạc bài gửi thôi :|
Vòng II
MẬT MÃ TOÁN HỌC
Câu 1. a) (5điểm) Cho dãy số [tex]1,3,6,10,15,..., \ \ \frac{n(n+1)}{2}[/tex]
Chứng tỏ rằng tổng của 2 số liên tiếp trong dãy luôn là số chính phương.
b) Một số tự nhiên có 5 chữ số. Nếu viết thêm 1 số vào bên trái hay bên phải số đó ta đều được một số có 6 chữ số. Biết rằng nếu viết thêm vào bên phải số đó thì được một số mới gấp 3 lần ta viết thêm vào bên trái. Hãy tìm số đó. (10điểm)
Câu 2 (15điểm). Phân tích đa thức thành nhân tử
a)[tex]x^4+6x^3+7x^2-6x+1[/tex]
b) [tex](x^2+y^2+z^2)(x+y+z)^2 + (xy+yz+xz)^2[/tex]
Câu 3.(15điểm) a) Cho [tex]a^3 - 3ab^2 = 19[/tex], [tex]b^3 - 3a^2b = 97[/tex]. Tính [tex]a^2+b^2[/tex]
b) Giải phương trình
Câu 4.(20điểm) Cho tứ giác ABCD. Đường thẳng qua A và song song với BC cắt BD ở E. Đường thẳng qua B và song song với AD cắt AC ở F. Chứng minh EF//DC.
Câu 5(25điểm). Cho hình thang cân ABCD có AB//CD, AB<CD. Độ dài đường cao BH bằng đường trung bình của hình thang ABCD. Chứng minh BD vuông góc với AC
Câu 6(10). Tìm giá trị lớn nhất hoặc nhỏ nhất của biểu thức:
[tex]B = -x^2 + 2xy - 4y^2 + 2x + 10y - 8[/tex]
[tex] C = \frac{x}{(x+10)^2}[/tex]
Chú ý:
Thí sinh gửi bài làm theo 2 cách sau:
Cách 1: Gửi trực tiếp bài giải cho hoa_giot_tuyet tại đây. <~ click
Cách 2: Soạn bằng file Word và gửi về email : thiensu_snowdrop@yahoo.com
Hạn chót nộp bài là ngày 20/3/2011
Để tránh hiện tượng SPAM và POST nhầm bài giải vào đây TOPIC sẽ được khóa.
Thanks
Ai gửi bài cho mik` rồi thì tks một cái nhá
Last edited by a moderator:

