[Toán 8] Hình

[vanmanh2001]

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

1)Cho tam giác ABC cân ở A có góc A = 108 độ Phân giác AD,BE . Chứng minh AD = 1/2 BE
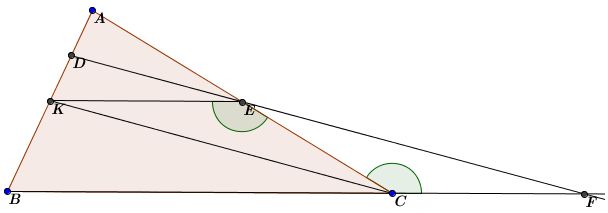
2)Cho tam giác ABC trên các cạnh AB , AC lần lượt lấy D và E sao cho AD = 1/4 AB; AE=1/2 AC.Đường thẳng DE cắt BC tại F.Chứng minh CF = 1/2 BC
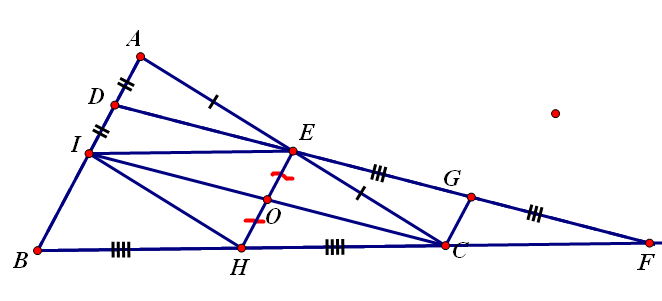
3)Cho tam giác ABC đường trung tuyến AM . Trên AM lấy D và E sao cho AD = DE = EM.Trên tia đối của CB lấy F sao cho CF = CM.Chứng minh 3 đường thẳng AC,BE,DF đồng quy

Câu hỏi event.

______________________
Các bạn có thể tham khảo thêm kiến thức: Tổng hợp các bài toán hình học 8 thường gặp

 

[harrypham]

2,

Lấy [TEX]K[/TEX] trung điểm [TEX]AB[/TEX]. Nối [TEX]K[/TEX] với [TEX]E[/TEX], [TEX]K[/TEX] với [TEX]C[/TEX]. Như vậy [TEX]D[/TEX] trung điểm [TEX]AK[/TEX].

Ta có do [TEX]KE[/TEX] là đường trung bình tam giác [TEX]ABC[/TEX] nên [TEX]KE//BC[/TEX] và [TEX]KE= \frac{1}{2}BC[/TEX].

Lại có [TEX]DE[/TEX] là đường trung bình tam giác [TEX]AKC[/TEX] nên [TEX]DE//KC[/TEX].

Xét tam giác [TEX]KEC[/TEX] và tam giác [TEX]FCE[/TEX] có
+ chung [TEX]CE[/TEX].
+ [TEX]\widehat{KEC}= \widehat{FCE}[/TEX] (so le trong do [TEX]KE//BC[/TEX])
+ [TEX]\widehat{ADE}= \widehat{ACK}[/TEX] (đồng vị) mà [TEX]\widehat{ADE}= \widehat{CEF}[/TEX] nên [TEX]\widehat{CEF}= \widehat{ACK}[/TEX].

Như vậy [TEX]\triangle KEC = \triangle FCE[/TEX] (g.c.g) nên [TEX]CF=EK[/TEX].
Mà [TEX]EK = \frac{1}{2}BC[/TEX] nên [TEX]CF = \frac{1}{2}BC[/TEX].
Ta có đpcm

 

[mikelhpdatke]

Bài 2:

Lấy $H$ là trung điểm của $BC$, $I$ là trung điểm của $AB$, $G$ là trung điểm của $EF$
Nối $I$ với $C$, $H$ với $E$, $C$ với $G$. $O$ là giao của $EH$ và $IC$
Dễ chứng minh được tứ giác $IECH$ là hình bình hành $\rightarrow EO=OH, IO=OC (1)$

Lại có $DE // IC (AD=DI, AE=EC) \rightarrow OC // EF (2)$

Từ $(1)$ và $(2)$ suy ra $HC=CF=BH \rightarrow CF= \frac{1}{2} BC$

 

[thaiha_98]

Bài 1:
Từ đầu bài ta suy ra được: $\angle BAD=\angle DAC=\angle BEA=54^o$, $\angle ABC=\angle ACB=36^o$
Do đó: $\angle ADB=90^o$ \Rightarrow $AD \perp BC$ \Rightarrow $BD=DC$
Trên $EC$ lấy điểm $F$ sao cho $EF=FC (F \in EC)$
Xét $\triangle CEB$ có: $EF=FC$ , $CD=DB$
\Rightarrow $DF$ là đường trung bình của $\triangle CEB$
\Rightarrow $\angle AFD=\angle BEA$ và $DF=\dfrac{1}{2}BE$ (1)
Mà $\angle BEA=\angle DAF (=54^o)$
\Rightarrow $\angle AFD=\angle DAF$ \Rightarrow $\triangle ADF$ cân tại $D$ \Rightarrow $AD=DF$ (2)
Từ (1) và (2) suy ra: $AD=\dfrac{1}{2}BE$

 

[luffy_1998]

3. Gọi D' là trung điểm của DF $\rightarrow D'C // AD, D'C = \dfrac{1}{2}DM = AD \rightarrow ADCD'$ là hình bình hành $\rightarrow DF$ đi qua trung điểm của AC.
E là trọng tâm $\triangle ABC \rightarrow BE$ đi qua trung điểm của AC.
Vậy DF, BE, BC đồng quy tại trung điểm của BC.