[Toán 8] Giúp em bài toán này với!

[sonexotic]

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

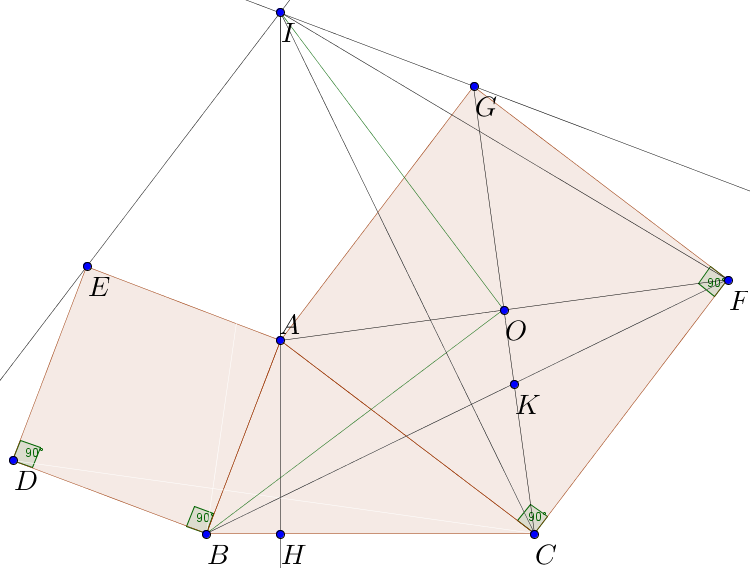
Cho tam giác ABC. Trên AB, AC và về phía ngoài tam giác ABC vẽ các hình vuông ABDE và ACFG. Vẽ hình bình hành mà 2 cạnh liên tiếp là AE và AG. Gọi đỉnh thứ 4 của hình bình hành là I.
a, Chứng minh rằng: I nằm trên đường thẳng chứa đường cao AH của tam giác ABC
b, Chứng minh rằng BF vuông góc CI, BF = CI
c, Chứng minh rằng AH, BF, DC đồng quy
d, Gọi O là tâm hình vuông AGFC. Chứng minh rằng OI vuông góc BO.

 

[harrypham]

a, Vì $\widehat{EAB}= \widehat{CAG}=180^o$ nên $\widehat{EAG}+ \widehat{BAC}=180^o$.
Lại có vì $EIGA$ là hình bình hành nên $\widehat{EAG}= \widehat{EAI}+ \widehat{EIA}$. Do đó $\widehat{EAG}+ \widehat{IEA}=180^o$. Như vậy $\widehat{BAC}= \widehat{IEA}$.
Dễ chứng minh $\triangle ABC= \triangle EAI$ (c.g.c) suy ra $AI=BC$ và $\widehat{ABH}= \widehat{EAI}$. Mà $\widehat{ABH}+ \widehat{BAH}=90^o$ nên $\widehat{EAI}+ \widehat{BAH}=90^o \implies \widehat{EAI}+ \widehat{BAH}+ \widehat{EAB}=180^o$.
Như vậy $A,I,H$ thẳng hàng.

b, Xét $\triangle IAC= \triangle BCF$ (c.g.c) vì $IA=BC$ (cm trên); $AC=CF$ (tc hình vuông); $\widehat{BCF}= \widehat{IAC}=90^o+ \widehat{C}$.
Do đó $BF=IC$ và $\widehat{BFC}= \widehat{ACI}$ mà $\widehat{ACI}+ \widehat{ICF}=90^o$ nên $\widehat{BFC}+ \widehat{ICF}=90^o$, hay $BF \perp IC$.

c, Chứng minh tương tự câu b ta có $DC \perp IB$.
Do đó $IA,CD,BF$ là trực tâm tam giác $IBC$ nên $AH,CD,BF$ đồng quy.

d, Vì $BF \perp IC$ nên $\widehat{ICK}= \widehat{OFB}$ (cùng phụ với $\widehat{OFK}$). Ta dễ chứng minh $\triangle OFB = \triangle OCI$ theo trường hợp c.g.c. Suy ra $\widehat{IOC}= \widehat{BOF} \implies \widehat{BOC}= \boxed{90^o}$.