[Toán 8]Củng cố kiến thức

[vitconxauxi_vodoi]

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

Câu 1:Cho biểu thức
A=[TEX]\frac{x+2}{x+3}-\frac{5}{x^2+x-6}+\frac{1}{2-x}[/TEX]
a,Rút gọn biểu thức A
b,Tìm x để A=[TEX]\frac{-3}{4}[/TEX]
c,Tìm x để biểu thức A nguyên
Câu 2:Phân tích đa thức thành nhân tử:
a,[TEX]3x^2+5x-2[/TEX]
b,[TEX]x^4-6x^3+12x^2-14x+3[/TEX]
c,[TEX]x^2-4xy-2x+4y+4y^2-35[/TEX]
Câu 3:
1,Xác định đa thức bậc 3 f(x) biết:
f(0)=-1 và f(x)-f(x-1)=x^2-x+1
2,Cho x,y,z là các số nguyên khác 0.Chứng minh rằng:
Nếu
a=x^2-yz
b=y^2-xz
c=z^2-xy
Thì (ax+by+cz) chia hết cho (a+b+c)
3,Tìm số nguyên dương n để [TEX]n^3-4n^2+4n-1[/TEX] có giá trị là số nguyên tố
Câu 4:
1,Chứng minh rằng phân số sau đây tối giản với mọi số tự nhiên n:

[TEX]\frac{2n+7}{3n+10}[/TEX]

[TEX]\frac{n^3+2n}{n^4+3n^2+1}[/TEX]

2,Tìm giá trị lớn nhất của biểu thức:

[TEX]A=-x^2+2xy-4y^2+2x+10y+5[/TEX]

3,Tìm số dư khi chia [TEX]22^{22}+55^{55}[/TEX] cho 7

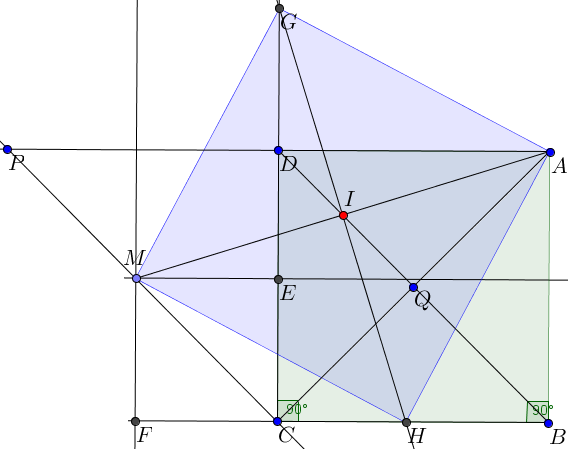
Câu 5: Cho hình vuông ABCD.Vẽ tia Cx là tia phân giác góc ngoài tại đỉnh C.Lấy điểm M trên tia Cx,vẽ [TEX]ME\perp DC[/TEX];[TEX]MF\perp BC[/TEX].Trên tia DC lấy G,trên tia đối của tia BC lấy H sao cho DG=BH=ME.Chứng minh:
a,Các tứ giác CEMF;AHMG là hình vuông
b,AM,HG,BD đồng quy.

 

[harrypham]

Câu 3. 3, [TEX]p=n^3-4n^2+4n-1=(n^3-1)-(4n^2-4n)=(n-1)(n^2+n+1)-4n(n-1)=(n-1)(n^2-3n+1)[/TEX] là số nguyên tố khi:
TH1. Với [TEX]n-1=1,n^2-3n+1=p[/TEX] Khi đó [TEX]n=2[/TEX] thì [TEX]n^2-3n+1=-1[/TEX] không là số nguyên tố.
TH2. Với [TEX]n-1=p,n^2-3n+1=1[/TEX] thì suy ra [TEX]n(n-3)=0 \Rightarrow n=3[/TEX]. Khi đó [TEX]p=3-1=2[/TEX].
Vậy để [TEX]p[/TEX] nguyên tố thì [TEX]n=3[/TEX].

Câu 4.
1, [TEX]A=\frac{2n+7}{3n+10}[/TEX]. Gọi [TEX](2n+7,3n+10)=d[/TEX].
Khi đó ta có [TEX]3(2n+7)-2(3n+10) \ \vdots d \Rightarrow 1 \ \vdots d \Rightarrow d=1[/TEX].
Vậy phân số [TEX]A[/TEX] tối giản.

[TEX]B=\frac{n^3+2n}{n^4+3n^2+1}[/TEX]. Đặt [TEX](n^3+2n,n^4+3n^2+1)=d[/TEX].
Ta có [TEX]n^3+2n \ \vdots d \Rightarrow n(n^3+2n) \ \ vdots d \Rightarrow n^4+2n^2 \ \vdots d[/TEX].
Lại có [TEX]n^4+3n^2+1 \ \vdots d \Rightarrow n^4+3n^2+1-(n^4+2n^2) \ \vdots d \Rightarrow n^2+1 \vdots d \Rightarrow n^3+n \ \vdots d \Rightarrow (n^3+2n)-(n^3+n) \vdots d \Rightarrow n \ \vdots d[/TEX].
Mà [TEX]n^4+3n^2+1 \ \vdots d \Rightarrow 1 \vdots d \Rightarrow d=1[/TEX]. Ta có đpcm.

2, [TEX]A=-x^2+2xy-4y^2+2x+10y+5[/TEX]
[TEX]=-x^2+2x(y+1)-(y+1)^2+(y+1)^2-4y^2+10y+5[/TEX]
[TEX]= -(x-y-1)^2-3y^2+12y+6[/TEX]
[TEX]= 2-(x-y-1)^2-3(y-2)^2 \le 2[/TEX].
[TEX]A=2 \Leftrightarrow \left \{ \begin{array} x-y-1=0 \\ y-2=0 \end{array} \right. \Leftrightarrow \left \{ \begin{array} y=2 \\ x=3 \end{array} \right.[/TEX]

3, [TEX]22^{22}+55^{55}[/TEX].
Ta có [TEX]22 \equiv 1 \pmod{7} \Rightarrow 22^{22} \equiv 1 \pmod{7}[/TEX]
Và [TEX]55 \equiv -1 \pmod{7} \Rightarrow 55^{55} \equiv -1 \pmod{7}[/TEX].
Do đó [TEX]22^{22}+55^{55} \equiv 0 \pmod{7}[/TEX] hay [TEX]22^{22}+55^{55}[/TEX] chia hết cho [TEX]7[/TEX].

 

[harrypham]

a, Tứ giác [TEX]MECF[/TEX] là hình chữ nhật có đường chéo [TEX]CM[/TEX] là phân giác góc [TEX]C[/TEX] nên [TEX]MECF[/TEX] là hình vuông.
Dễ chứng minh [TEX]\triangle ADG= \triangle ABH[/TEX] (c.g.c) suy ra [TEX]AH=AG[/TEX] và [TEX]\widehat{HAB}= \widehat{GAD}[/TEX], mà [TEX]\widehat{HAB}+ \widehat{DAH}=90^o \Rightarrow \widehat{GAD}+ \widehat{DAH}=90^o \Rightarrow \widehat{GAH}=90^o[/TEX].
Chứng minh tương tự [TEX]MH=HA[/TEX] và [TEX]MH=MG[/TEX] suy ra tứ giác [TEX]MGAH[/TEX] là hình thoi có [TEX]\widehat{GAH}=90^o[/TEX] nên [TEX]MGAH[/TEX] là hình vuông.

b, Vì [TEX]MGAH[/TEX] là hình vuông nên [TEX]AM[/TEX] và [TEX]HG[/TEX] cắt nhau tại trung điểm mỗi đường.
Đặt [TEX]I= AM \cap HG[/TEX], [TEX]Q= BD \cap AC[/TEX].
Kéo dài [TEX]AD[/TEX] cắt [TEX]CM[/TEX] tại [TEX]P[/TEX].

Ta có [TEX]DB \parallel PC[/TEX] hay [TEX]DQ \parallel PC[/TEX], mà [TEX]Q[/TEX] trung điểm [TEX]AC[/TEX] nên [TEX]D[/TEX] trung điểm [TEX]AP[/TEX].

Xét tam giác [TEX]APM[/TEX] có [TEX]I[/TEX] trung điểm [TEX]AM[/TEX], [TEX]D[/TEX] trung điểm [TEX]AP[/TEX] nên [TEX]ID \parallel PM[/TEX] hay [TEX]ID \parallel PC[/TEX].
Mà [TEX]DB \parallel PC[/TEX] nên [TEX]D,I,B[/TEX] thẳng hàng. Suy ra [TEX]AM,HG,BD[/TEX] đồng quy tại [TEX]I[/TEX].