L
locxoaymgk
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Vào đây nhá:
----------------------------------------------------------------------------------------------
http://diendantoanhoc.net/forum/index.php?showtopic=41380
Cách đặt ẩn phụ này rất hay và có nhiều ứng dụng !!!!!!
Ta có [TEX]2.2(a^4+b^4) \geq 2.(a^2+b^2)^2 \ \ (1)[/TEX]
Mà[TEX] 2(a^2+b^2) \geq (a+b)^2= 16 \Rightarrow a^2+b^2 \geq 8 \ \(2)[/TEX]
Từ [TEX](1) \ \ va \ \ (2) \Rightarrow a^4+b^4 \geq 32[/TEX]
Cách này cũng gọn hơn cách đặt ẩn phụ nhưng Cách đặt ẩn phụ cũng là một cách CM BDT rất hay!!
Cách 1: có trả lời rồi
Cách 2: trong địa chỉ link
Cách 3: Áp dụng [TEX]BDT 3(a^2+b^2+c^2) \geq (a+b+c)^2[/TEX]
----------------------------------------------------------------------------------------------
http://diendantoanhoc.net/forum/index.php?showtopic=41380
Cách đặt ẩn phụ này rất hay và có nhiều ứng dụng !!!!!!
P/s: Bài 1 không nhất thiết đặt ẩn phụ cho nó rắc rối:Ví dụ 1 .CMR Vớivầ+b=4 thì a^4+b^4=32
Nhận xét rằng một biểu thức nhiều biến thường đạt giá trị lớn nhất hay nhỏ nhất khi tất cả các biến bằng nhau ( tổng quát hơn là trường hợp một số biến bằng nhau) hoặc một số biến có giá trị trên biên .Điều này gợi ý cho ta cách đổi biến như sau
Lời giải Do [TEX]a+b=4 [/TEX] nên có thể đặt [TEX]a=2+x[/TEX] với [TEX]b=2-x [/TEX]với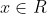
Ta có(dpcm)^{4}+(2-x)^{4}=2x^{4}+48x^{2}+32%20\geq%2032)
Đẳng thức xảy ra
Ta có [TEX]2.2(a^4+b^4) \geq 2.(a^2+b^2)^2 \ \ (1)[/TEX]
Mà[TEX] 2(a^2+b^2) \geq (a+b)^2= 16 \Rightarrow a^2+b^2 \geq 8 \ \(2)[/TEX]
Từ [TEX](1) \ \ va \ \ (2) \Rightarrow a^4+b^4 \geq 32[/TEX]
Cách này cũng gọn hơn cách đặt ẩn phụ nhưng Cách đặt ẩn phụ cũng là một cách CM BDT rất hay!!
Bài này có 3 cách giải!!
Cách 1: có trả lời rồi
Cách 2: trong địa chỉ link
Cách 3: Áp dụng [TEX]BDT 3(a^2+b^2+c^2) \geq (a+b+c)^2[/TEX]
