 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Giải hộ em bài 5 câu c....
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Bạn vẽ hình ra giùm mình được không ???Giải hộ em bài 5 câu c....
Cho mình hỏi bạn đã học tam giác đồng dạng chưa???Đây là nháp nhá!!! Chữ xấu cố dịch nha còn nội dung thì t nghĩ là đúng r á"
Rồi bạn. Năm nay mk lên lớp 9Cho mình hỏi bạn đã học tam giác đồng dạng chưa???
Giải hộ em bài 5 câu c....
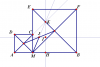
Câu d nữa.... helpView attachment 17755
Lấy $K$ là giao điểm của $AC$ và $BE$, $H$ là hình chiếu của $K$ trên $AB$, $I$ là giao đường thẳng song song với $AB$ kẻ tại $J$ và $KH$
Chứng minh được $K,J,M$ thẳng hàng và $J$ là trung điểm $KM$
Có $\triangle AKB$ vuông cân tại $K$ nên $KH=\dfrac12 AB$
Lại có trong $\triangle KMH$ có $JK=JM$ và $JI // MH$ nên $IK=IH$ hay $IJ$ là đường trung bình
$\Rightarrow IH=\dfrac14 AB$
Vậy tập hợp điểm $I$ là đường thẳng song song với $AB$ được giới hạn bởi $AD$ và $BF$ và cách $AB$ 1 khoảng bằng $\dfrac14 AB$
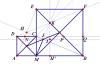
c,Trong làm bài thì câu c) nên để tên khác $H$ nhé vì có liên quan câu d)
View attachment 17765
Xét $\triangle DNA \sim \triangle HNC \Rightarrow DN \ / \ NA = HN \ / \ CN \Rightarrow \triangle HDN \sim \triangle CAN $
$\Rightarrow \angle DHA =\angle DCA=45^o$
Tương tự: $\triangle HCA \sim \triangle KCB \Rightarrow \triangle HCK \sim \triangle ACB \Rightarrow \angle KHC =45^o$
$\Rightarrow D,H,K$ thẳng hàng (1)
Lại có $CD=PQ \Rightarrow DP=CQ=EF$, mà $DP // EF \Rightarrow DEFP$ là hình bình hành
Mặt khác: $\angle ECK=\angle CEK, \angle KCP=\angle KPC \Rightarrow EK=KP=CP \Rightarrow K$ là trung điểm $EP$
$\Rightarrow K$ cũng là trung điểm của $DF \Rightarrow D,K,F$ thẳng hàng (2)
Từ (1) và (2) suy ra $D,H,F$ thẳng hàng

