giúp em ạ
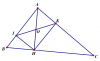
cho tam giác ABC vuông góc ở A . kẻ đường cao AH .gọi I và K lần lượt là hình chiếu của điểm H trên AB và AC.a, C/m HI vuông góc vs HK
b, c/m IA=HK
C, cm IK=AH
d, gọi O la giao điểm của AH và IK. Cm OI=OK=OA=OH
a) Tam giác HKC vuông tại K => [tex]\widehat{HKC}+\widehat{C} = 90^{\circ}[/tex]
Tam giác AHC vuông tại H => [tex]\widehat{HAC}+\widehat{C} = 90^{\circ}[/tex]
=> [tex]\widehat{KHC}=\widehat{HAC}[/tex]
[tex]\widehat{BIH}=\widehat{ABC}= 90^{\circ}[/tex] , mà 2 góc này ở vị trí đồng vị
=> AK // HI
=> [tex]\widehat{AHI}=\widehat{HAC}[/tex] ( 2 góc slt)
nên [tex]\widehat{AHI}=\widehat{KHC}=> \widehat{AHI}+\widehat{AHK}=\widehat{KHC}+\widehat{AHK}=> \widehat{IHK}=\widehat{AHC}[/tex] [tex]\widehat{AHI}=\widehat{KHC}=> \widehat{AHI}+\widehat{AHK}=\widehat{KHC}+\widehat{AHK}=> \widehat{IHK}=\widehat{AHC}[/tex]
mà [tex]\widehat{AHC}=90^{\circ} => \widehat{IHK}=90^{\circ}[/tex] [tex]\widehat{AHC}=90^{\circ} => \widehat{IHK}=90^{\circ}[/tex] [tex]\widehat{AHC}=90^{\circ} => \widehat{IHK}=90^{\circ}[/tex]
b) Cm: tam giác AIH = tam giác HKA (cạnh huyền - góc nhọn) => IA = HK
c) Cm: tam giác IAK = tam giác HKA ( cgc)
[tex]\widehat{IAK}=\widehat{HKA}=90^{\circ}[/tex]
AK chung
IA = HK ( cmt)
=> IK = AH
d) Có [tex]\widehat{BAC}=\widehat{HKC}=90^{\circ}[/tex] mà 2 góc này ở vị trí đồng vị
=> AI // HK
=> [tex]\widehat{IAO}=\widehat{OHK}[/tex]
[tex]\widehat{AIO}=\widehat{OKH}[/tex]
CM: tam giác AOI = tam giác HOK (gcg) => OA = OH
=> O là trung điểm của AH , mà AH = IK
=> O là trung điểm của IK
=> OA = OH = OI = OK
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
