[Toán 7] PHƯƠNG PHÁP CHỨNG MINH HÌNH HỌC

0872 · 26 Tháng bảy 2013

Phương pháp chứng minh hình học

A. Lý thuyết

- Chứng minh bài toán hình học là dựa vào những điều kiện đã biết ( giả thiết, định nghĩa, tiên đề, định lý) đã học và suy luận để chứng tỏ kết luận của bài toán đúng

B. Cách chứng minh hình học

1. Nghiên cứu đề toán

Đọc kĩ đề bài và hiểu rõ:
- Đề bài cho những điều kiện gì?
- Đề bài yêu cầu chứng minh gì?

[TEX]\Rightarrow[/TEX] Từ đó tóm tắt đề bài

2. Tìm hiểu nội dung giả thiết

- Từ nội dung giả thiết, ta có thể suy ra tính chất gì?

VD:

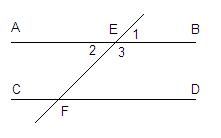
Đề bài cho [TEX]AB // CD[/TEX]

[TEX]\Rightarrow \hat{E}_1= \hat{F}_1[/TEX], [TEX]\hat{E}_2=\hat{F}_1[/TEX], [TEX]\hat{E}_3=\hat{F}_1=180^o[/TEX] ...

3. Tìm hiểu nội dung của kết luận

- Để đi đến kết luận, ta cần chứng minh điều gì?
- Trong các điều đó, điều nào đã biết, điều nào cần chứng minh?

VD:

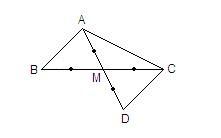
Đề bài: Chứng minh [tex]\large\Delta_{ABM} = \large\Delta_{DMC}[/tex]. Biết MB = MC, MD = MA

[TEX]\Rightarrow[/TEX] Ta cần chứng minh [TEX]\widehat{AMB} = \widehat{AMC}[/TEX]

4. Nối từ giả thiết đến kết luận

Trong quá trình tìm lời giải, ta thường dùng phương pháp phân tích đi lên:

- Để chứng minh A (kết luận) , ta phải chứng minh B
- Để chứng minh C, ta tìm cách chứng minh D, rồi cuối cùng tìm cách chứng minh H

-Nếu từ giả thiết mà ta chứng minh được H thì ta đã tìm được cách giải bài toán bằng cách nối giả thiết đến kết luận

A [TEX]\Rightarrow[/TEX] H [TEX]\Rightarrow[/TEX] ... [TEX]\Rightarrow[/TEX] D [TEX]\Rightarrow[/TEX]C

VD:

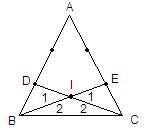
Cho hình vẽ trên. Chứng minh [TEX]\large\Delta_{BIC}[/TEX] là tam giác cân

* Giả thiết:
[TEX]\large\Delta_{ABC}[/TEX]

[TEX]AD = AE[/TEX]

[TEX]BD = CE[/TEX]

* Kết luận:
[TEX]\large\Delta_{BIC}[/TEX] cân

* Phân tích đi lên:
- Để chứng tỏ [TEX]\large\Delta_{BIC}[/TEX] cân, ta cần chứng minh [TEX]\hat{B}_2 = \hat{C}_2[/TEX]
- Ta đã biết [TEX]\hat{B}=\hat{C}[/TEX] nên để chứng minh [TEX]\hat{B}_2 = \hat{C}_2[/TEX], ta cần chứng minh [TEX]\hat{B}_1 = \hat{C}_1[/TEX]. Muốn vậy cần chứng minh [TEX]\large\Delta_{ABE} = \large\Delta_{ADC}[/TEX]

- [TEX]\large\Delta_{ABE} = \large\Delta_{ADC}[/TEX] theo trường hợp cạnh - góc - cạnh

0872 · 26 Tháng bảy 2013

C. Cách trình bày bài toán chứng minh hình học

- Sau khi vẽ hình, ghi kí hiệu, ghi giả thiết kết luận, ta trình bày chứng minh theo trình tự ngược lại của bước phân tích đi lên, tức là ta trình bày lời giải theo phương pháp tổng hợp.

Chẳng hạn trình bày lời giải ở ví dụ phần 4 (B) như sau:

[TEX]\large\Delta{ABE}[/TEX] và [TEX]\large\Delta{ACD}[/TEX] có:

[TEX]AE = AD[/TEX] (giả thiết)

[TEX]\hat{A}[/TEX] là góc chung

[TEX]AB=AB[/TEX] (tổng của hai đoạn thẳng bằng nhau)

[TEX]\Rightarrow \large\Delta{ABE} = \large\Delta{ACD} (c.g.c) \Rightarrow \hat{B}_1 = \hat{C}_1[/TEX]

[TEX]\large\Delta{ABC}[/TEX] có [TEX]AB = AC[/TEX] nên là tam giác cân

[TEX]\Rightarrow \hat{B} = \hat{C}[/TEX]

[TEX]\Rightarrow \hat{B}-\hat{B}_1 = \hat{C}-\hat{C}_1[/TEX]

[TEX]\Rightarrow \hat{B}_2=\hat{C}_2[/TEX]

[TEX]\large\Delta{BIC}[/TEX] có hai góc bằng nhau nên là tam giác cân

D. Cách trình bày bài toán chứng minh hình học theo phương pháp phản chứng

- Một số bài toán hình học được chứng minh bằng phương pháp phản chứng

- Chứng minh phản chứng gồm 3 bước:

Bước 1: Phủ định kết luận (Giả sử có điều trái với kết luận của bài toán.
Bước 2: Đưa đến mâu thuẫn (Từ điều giả sử trên, từ giả thiết của bài toán và các kiến thức đã học, ta suy ra điều mâu thuẫn với giả thiết hay một kiến thức đã học
Bước 3: Khẳng định kết luận (Vậy kết luận bài toán là đúng)

VD: CMR từ tiên đề Ơ- clit ta suy ra : Nếu hai đường thẳng // với một đường thẳng thứ 3 thì 2 đường thẳng //

* Giả thiết:

a//c
b//c

* Kết luận: a // b

- Bước 1: Giả sử a không // với b
- Bước 2: Vậy a và b cắt nhau tại một điểm, gọi giao điểm đó là M. Qua M ta có hai đường thẳng phân biệt a và b // với đường thẳng c, điều này mâu thuẫn với tiên đề Ơ- clit
- Bước 3: Vậy a // b

Tìm kiếm

Tìm kiếm

[Toán 7] PHƯƠNG PHÁP CHỨNG MINH HÌNH HỌC

0872

0872