[Toán 7] Đề thi

[nguynteucphuong]

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

1.a) Chứng tỏ [tex]7^6+7^5-7^4[/tex] chia hết cho 55.

b) Tính [tex]A= 1+5+5^2+5^3+...+5^{49}+5^{50}.[/tex]

2. Tìm x, y biết: [tex]\frac{1+3y}{12}=\frac{1+5y}{5x}=\frac{1+7y}{4x}[/tex]

3. Một vật chuyển động trên các cạnh hình vuông. Trên hai cạnh đầu vật đó chuyển động với vận tốc 5m/s, trên cạnh thứ ba với vận tốc 4m/s, trên cạnh thứ tư với vận tốc 3m/s. Hỏi độ dài cạnh hình vuông? Biết tổng thời gian chuyển động trên 4 cạnh hình vuông là 59".

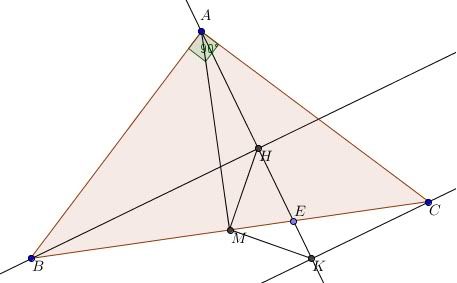
4. Cho tam giác ABC vuông cân tại A, M là trung điểm của BC, điểm E nằm giữa M và C. Kẻ BH và CK vuông góc với AE ( H và K thuộc AE). Chứng minh rằng:
a) BH= AK
b) Tam giác MBH=MAK
c) Tam giác MHK vuông cân.

5. Tìm x,y biết: [tex]25-y^2=8(x-2009)^2[/tex]

Mod edit. chú ý latex( học gõ tại ĐÂY)+cách đặt tiêu đề ( [toán 7] + tiêu đề )

 

[harrypham]

1.a) Chứng tỏ [tex]7^6+7^5-7^4[/tex] chia hết cho 55.

[TEX]7^6+7^5-7^4=7^4(7^2+7-1)=7^4.55 \ \vdots 55[/TEX].

b) Tính [tex]A= 1+5+5^2+5^3+...+5^{49}+5^{50}.[/tex]

Ta có [TEX]5A= 5+5^2+...+5^{51} [/TEX]
[TEX]\Rightarrow 5A-A= 5^{51}-1 \Rightarrow \fbox{A= \frac{5^{51}-1}{4}}[/TEX]

2. Tìm x, y biết: [tex]\frac{1+3y}{12}=\frac{1+5y}{5x}=\frac{1+7y}{4x}[/tex]

 

[harrypham]

4. Cho tam giác ABC vuông cân tại A, M là trung điểm của BC, điểm E nằm giữa M và C. Kẻ BH và CK vuông góc với AE ( H và K thuộc AE). Chứng minh rằng:
a) BH= AK
b) Tam giác MBH=MAK
c) Tam giác MHK vuông cân.
[/B]

a) Xét tam giác BHA và tam giác AKC có

• Xét tam giác ABH vuông tại H có [TEX]\widehat{ABH}+ \widehat{BAH}=90^o[/TEX].
  Mà [TEX]\widehat{BAH}+ \widehat{HAC}=90^o[/TEX]
  [TEX]\Rightarrow \widehat{HAC}= \widehat{BAH}[/TEX]
• [TEX]AC=AB[/TEX] (gt)

[TEX]\Rightarrow \bigtriangleup BHA= \bigtriangleup AKC[/TEX] (cạnh huyền - góc nhọn)
[TEX]\Rightarrow BH=AK[/TEX].

b) Ta dễ dàng chứng minh được tam giác AMB vuông cân tại M.
Do [TEX]BH \perp AK, \ CK \perp AK \Rightarrow BH//CK \Rightarrow \widehat{HBE}= \widehat{ECK}[/TEX].

Xét hai tam giác AME và CEK có
+ Hai góc E đối đỉnh
+ [TEX]\widehat{AMC}= \widehat{CKE}=90^o[/TEX]
[TEX]\Rightarrow \widehat{MAK}= \widehat{ECK}[/TEX].
Mà [TEX]\widehat{HBE}= \widehat{ECK}[/TEX]
[TEX]\Rightarrow \widehat{MAK}= \widehat{HBE}[/TEX].

Dễ dàng chứng minh được tam giác BMH và tam giác AMK bằng nhau theo c.g.c

c) Do [TEX]\bigtriangleup BMH= \bigtriangleup AMK \Rightarrow MH=MK \ \ \ (1)[/TEX]
Cũng vì [TEX]\bigtriangleup BMH= \bigtriangleup AMK \Rightarrow \widehat{BMH}= \widehat{AMK} \Rightarrow \widehat{BMA}= \widehat{HMK}=90^o[/tex]
Vậy [TEX]\widehat{HMK}=90^o \ \ \ \ \ (2)[/TEX]

Từ (1) và (2) ta có đpcm.